Question

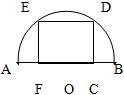已知以AB为直径的半圆有一个内接正方形CDEF，其边长为1（如图）设AC=a，BC=b，作数列u₁=a-b，u₂=a²-ab+b²，u₃=a³-a²b+ab²-b³，…，u_k=a^k-a^k-1b+a^k-2b²-…+（-1）^kb^k；
求证：u_n=u_n-1+u_n-2（n≥3）．

Answer 1

分析：要证u_n=u_n-1+u_n-2（n≥3），利用题目中给出的信息先求出通项u_n，然后利用圆中直角三角形的几何性质建立u_n，u_n-1，u_n-2三者的关系，即可得证．

解答：证明：通项公式可写成
u_k=a^k-a^k-1b+a^k-2b²-+（-1）^kb^k=

ak+1-(-1)k+1bk+1

a+b

因a-b=AC-BC=AC-AF=FC=1，
ab=AC•BC=CD²=1．
故得un-2=

an-1-(-1)n-1bn-1

a+b

，n≥3
=ab

an-1-(-1)n-1bn-1

a+b

=

anb-(-1)n-1abn

a+b

，
un-1=

an-(-1)nbn

a+b

=(a-b)

an-(-1)nbn

a+b

=

an+1-anb-(-1)nabn-(-1)n+1bn+1

a+b

于是有un-1+un-2=

an+1-(-1)n+1bn+1

a+b

=un．n≥3

点评：本题是个中档题，主要考查了由数列递推式求数列的通项，以及证明等式的方法，在证明过程中注意几何图形的几何性质的应用．