题目内容
如图,已知⊙O中,直径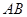 垂直于弦
垂直于弦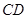 ,垂足为
,垂足为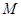 ,
,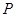 是
是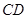 延长线上一点,
延长线上一点, 切⊙O于点
切⊙O于点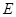 ,连接
,连接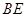 交
交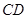 于点
于点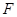 ,证明:
,证明:
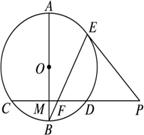
(1)  ;
;
(2) 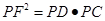 .
.
【答案】
(1)证明过程详见解析;(2)证明过程详见解析.
【解析】
试题分析:本题以圆为几何背景考查边和角的关系,考查学生的转化能力.第一问,利用 是圆的切线,得
是圆的切线,得 ,又利用
,又利用 ,得
,得 ,最后由于
,最后由于 是等腰三角形,所以
是等腰三角形,所以 ,所以得
,所以得 ;第二问,利用切线的性质可得
;第二问,利用切线的性质可得 ,而利用第一问的结论,可得
,而利用第一问的结论,可得 ,所以
,所以 .
.
试题解析:(1)连接 ,∵
,∵ 切
切 于点
于点 ,∴
,∴ ,
,
∴ ,
,
又∵ ,
,
∴ ,
,
又∵ ,
,
∴ .
5分
.
5分
(2) ∵ ,
,
∴ ,
,
∴
又∵ ,
,
∴ .
10分
.
10分
考点:1.切线的性质;2.等腰三角形和直角三角形中边和角的关系;3.对顶角相等.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
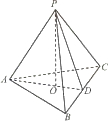 如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2
如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2



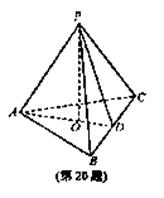 (Ⅱ)在线段AP上是否存在点M,使得二面角A-MC-B为直二面角?若存在,求出AM的长;若不存在,请说明理由。
(Ⅱ)在线段AP上是否存在点M,使得二面角A-MC-B为直二面角?若存在,求出AM的长;若不存在,请说明理由。