题目内容
（2010•济南一模）已知：|
|=3，|
|=2，＜
，
＞=60°，则|2
+
|=
| a |
| b |
| a |
| b |
| a |
| b |
2
| 13 |
2
．| 13 |
分析：由题设条件，对|2
+
|进行平方，先出和向量模的平方，再开方求两者和的模．
| a |
| b |
解答：解：∵：|
|=3，|
|=2，＜
，
＞=60°，
∴
•
=|
||
|cos＜
，
＞=3×2×
=3，
所以|2
+
|2=4
2+4
+
2=52，
故|2
+
|=2
．
故答案为：2
．
| a |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
所以|2
| a |
| b |
| a |
| a |
| •b |
| b |
故|2
| a |
| b |
| 13 |
故答案为：2
| 13 |
点评：本题考查向量模的求法，对向量的求模运算，一般采取平方方法表示成向量的内积，根据内积公式求出其平方，再开方求模，本题是向量中的基本题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
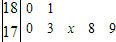（2010•济南一模）一次选拔运动员，测得7名选手的身高（单位cm）分布茎叶图如图，记录的平均身高为177cm，有一名候选人的身高记录不清楚，其末位数记为x，那么x的值为（ ）