题目内容
1.函数f(x)=x3-ax-1.(1)当a=8时,求函数f(x)在x=0处的切线方程.
(2)讨论f(x)=x3-ax-1的单调性.
分析 (1)求出函数的导数,计算f(0),f′(0),求出切线方程即可;
(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可.
解答 解:(1)a=8时,f(x)=x3-8x-1,f′(x)=3x2-8,
故f′(0)=-8,f(0)=-1,
故切线方程是:y+1=-8x,
即8x+y+1=0;
(2)f′(x)=3x2-a,
a≤0时,f′(x)≥0,f(x)在R递增,
a>0时,令f′(x)>0,解得:x>$\sqrt{\frac{a}{3}}$或x<-$\sqrt{\frac{a}{3}}$,
令f′(x)<0,解得:-$\sqrt{\frac{a}{3}}$<x<$\sqrt{\frac{a}{3}}$,
故f(x)在(-∞,-$\sqrt{\frac{a}{3}}$)递增,在(-$\sqrt{\frac{a}{3}}$,$\sqrt{\frac{a}{3}}$)递减,在($\sqrt{\frac{a}{3}}$,+∞)递增.
点评 本题考查了函数的单调性问题,考查导数的应用以及分类讨论思想,考查切线方程,是一道中档题.

练习册系列答案
相关题目
11.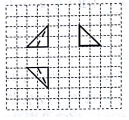 如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
 如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )| A. | 2+2$\sqrt{3}$+$\sqrt{6}$ | B. | 4+2$\sqrt{3}$+$\sqrt{6}$ | C. | 4+4$\sqrt{3}$+$\sqrt{6}$ | D. | 2+$\sqrt{3}$+$\sqrt{6}$ |
16.假设有两个分类变量X与Y,它们的可能取值分别为{x1,x2}和{y1,y2},其2×2列联表则当m取下面何值时,X与Y的关系最弱?( )
| y1 | y2 | |
| x1 | 10 | 18 |
| x2 | m | 26 |
| A. | 8 | B. | 9 | C. | 14 | D. | 19 |
1.长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,点E是BB1的中点,则D1A与平面AEC所成角的余弦值为( )
| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{\sqrt{6}}}{5}$ | D. | $\frac{{\sqrt{13}}}{5}$ |
8.函数y=sinx-2x的导数是( )
| A. | cosx-2x | B. | cosx-2x•ln2 | C. | -cosx+2x | D. | -cosx-2x•ln2 |
6.函数f(x)=$\frac{lg({x}^{2}-1)}{\sqrt{{x}^{2}-x-2}}$的定义域为( )
| A. | (-∞,-2)∪(1,+∞) | B. | (-2,1) | C. | (-∞,-1)∪(2,+∞) | D. | (1,2) |