题目内容
已知x2+px+q<0的解集为{x|-2<x<3},若f(x)=qx2+px+1
(1)求不等式f(x)>0的解集;
(2)若f(x)<
恒成立,求a的取值范围.
(1)求不等式f(x)>0的解集;
(2)若f(x)<
| a |
| 6 |
(1)∵求不等式x2+px+q<0的解集为{x|-2<x<3},
∴-2,3是对应方程x2+px+q=0的两个根,
则
,解得
,
即f(x)=qx2+px+1=-6x2-x+1,
由f(x)>0得-6x2-x+1>0,
即6x2+x-1<0,
(2x+1)(3x-1)<0,
解得-
<x<
,
即不等式f(x)>0的解集是(-
,
),
(2)若f(x)<
恒成立,即球f(x)的最大值即可,
∵f(x)=-6x2-x+1=-6(x+
)2+
,
∴当x=-
时,f(x)的最大值为
,
∴要使若f(x)<
恒成立,
则
<
,
即a>
,
即a的取值范围(
,+∞).
∴-2,3是对应方程x2+px+q=0的两个根,
则
|
|
即f(x)=qx2+px+1=-6x2-x+1,
由f(x)>0得-6x2-x+1>0,
即6x2+x-1<0,
(2x+1)(3x-1)<0,
解得-
| 1 |
| 2 |
| 1 |
| 3 |
即不等式f(x)>0的解集是(-
| 1 |
| 2 |
| 1 |
| 3 |
(2)若f(x)<
| a |
| 6 |
∵f(x)=-6x2-x+1=-6(x+
| 1 |
| 12 |
| 25 |
| 24 |
∴当x=-
| 1 |
| 12 |
| 25 |
| 24 |
∴要使若f(x)<
| a |
| 6 |
则
| 25 |
| 24 |
| a |
| 6 |
即a>
| 25 |
| 4 |
即a的取值范围(
| 25 |
| 4 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的解集是
的解集是 ,则
,则 的值是( )
的值是( )



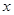 的方程
的方程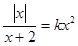 有四个不同的实数解,则实数
有四个不同的实数解,则实数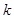 的取值范围为()
的取值范围为() 


