题目内容
若关于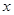 的方程
的方程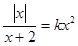 有四个不同的实数解,则实数
有四个不同的实数解,则实数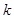 的取值范围为()
的取值范围为()
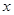 的方程
的方程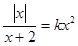 有四个不同的实数解,则实数
有四个不同的实数解,则实数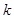 的取值范围为()
的取值范围为() A. | B. | C. | D. |

试题分析:要求
 ,方程化为
,方程化为 ,
,显然
 满足上述方程,是方程的一个根
满足上述方程,是方程的一个根若

则方程两边同除以
 有
有
若
 则方程变为
则方程变为 ,即
,即
若
 则方程变为
则方程变为 即
即
若
 ,(1)(2)均无解。显然
,(1)(2)均无解。显然 不是(1)(2)的解
不是(1)(2)的解若方程有四个不同的实数根,之前已得到
 是原方程的根,则要求方程(1)(2)有3个根
是原方程的根,则要求方程(1)(2)有3个根对(1)若判别式
 ,则
,则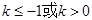 .
.对(2)若判别式
 ,解得
,解得 ,
,前已分析

若
 ,则(1)有两个不相等实根,两根之积为
,则(1)有两个不相等实根,两根之积为 ,两根之和为
,两根之和为 ,说明两根均为负值,但(1)方程前提条件是
,说明两根均为负值,但(1)方程前提条件是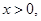 ,因此
,因此 时方程(1)在
时方程(1)在 前提下无解,原方程不可能有4个不同的实数根。
前提下无解,原方程不可能有4个不同的实数根。若
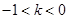 ,(1)方程无根,原方程不可能有4个不同的实数根。
,(1)方程无根,原方程不可能有4个不同的实数根。若
 ,(2)方程无根,原方程不可能有4个不同的实数根。
,(2)方程无根,原方程不可能有4个不同的实数根。若
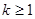 ,方程(1)有两个不相等实根,两根之积为
,方程(1)有两个不相等实根,两根之积为 ,两根之和为
,两根之和为 ,说明有一个正根一个负根,在
,说明有一个正根一个负根,在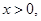 前提下,只有一个正根,则要求(2)有两个不相等的负根。则
前提下,只有一个正根,则要求(2)有两个不相等的负根。则 .要求
.要求 .
.对于(2)此时判别式
 ,两根之和为
,两根之和为 , 两根之积
, 两根之积 ,说明(2)有两个不相等的负根,之前要求
,说明(2)有两个不相等的负根,之前要求 ,对(2),若
,对(2),若 ,则
,则 ,显然
,显然 不是方程的根。
不是方程的根。综上所述,要求
 .
.
练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
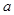 2+
2+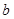 2恒成立,试求2
2恒成立,试求2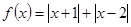 的最小值为
的最小值为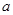 .
.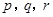 为正实数,且
为正实数,且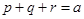 ,求证:
,求证: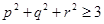 .
.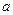 克,现在向糖水中再加
克,现在向糖水中再加 克糖,此时糖水变得更甜了.(其中
克糖,此时糖水变得更甜了.(其中 ).
).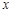 的不等式
的不等式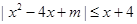 的解集为
的解集为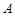 ,且
,且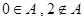 ,则实数
,则实数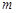 的取值范围是 .
的取值范围是 .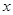 使
使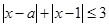 成立,则实数
成立,则实数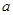 的取值范围_______
的取值范围_______