题目内容
若函数f(x)=
的定义域为R,则实数k的取值范围是______.
| x2+6kx+k+8 |
∵函数f(x)=
的定义域为R,
∴不等式x2+6kx+k+8≥0对任意x∈R恒成立,
可得△=36k2-4(k+8)≤0,解之得-
≤k≤1
即k的取值范围是{k丨-
≤k≤1}
故答案为:{k丨-
≤k≤1}
| x2+6kx+k+8 |
∴不等式x2+6kx+k+8≥0对任意x∈R恒成立,
可得△=36k2-4(k+8)≤0,解之得-
| 8 |
| 9 |
即k的取值范围是{k丨-
| 8 |
| 9 |
故答案为:{k丨-
| 8 |
| 9 |

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
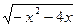 ≤
≤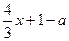 的解集是[-4,0],则a的取值范围是( )
的解集是[-4,0],则a的取值范围是( )





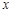 的不等式
的不等式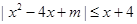 的解集为
的解集为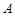 ,且
,且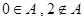 ,则实数
,则实数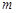 的取值范围是 .
的取值范围是 .