题目内容
过抛物线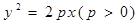 的对称轴上一点
的对称轴上一点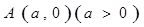 的直线与抛物线相交于M、N两点,自M、N向直线
的直线与抛物线相交于M、N两点,自M、N向直线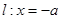 作垂线,垂足分别为
作垂线,垂足分别为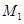 、
、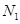 。
。
(Ⅰ)当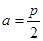 时,求证:
时,求证: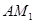 ⊥
⊥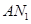 ;
;
(Ⅱ)记
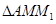 、
、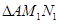 、
、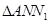 的面积分别为
的面积分别为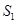 、
、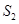 、
、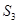 ,是否存在
,是否存在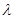 ,使得对任意的
,使得对任意的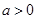 ,都有
,都有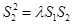 成立。若存在,求
成立。若存在,求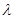 值;若不在,说明理由。
值;若不在,说明理由。
【答案】
(Ⅰ)略
(Ⅱ)存在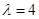 ,使得对任意的
,使得对任意的 ,都有
,都有 成立,证明略
成立,证明略
【解析】解:本小题主要考察抛物线的定义和几何性质等平面解析几何的基础知识,
考查综合运用数学知识进行推理运算的能力。(12分)
依题意,可设直线MN的方程为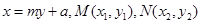 ,则有
,则有

由 消去x可得
消去x可得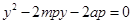 ……………2分
……………2分
从而有 ①
①
于是 ②
②
又由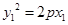 ,
, 可得
可得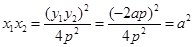 ③…………4分
③…………4分
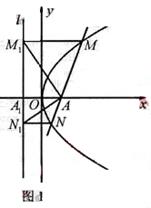
(Ⅰ)如图1,当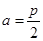 时,点
时,点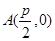 即为抛物线的焦点,
即为抛物线的焦点,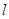 为其准线
为其准线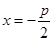
此时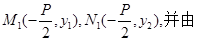 ①可得
①可得  ……………5分
……………5分
证法1: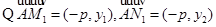
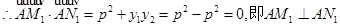 ……………6分
……………6分
证法2:

 …………6分
…………6分

(Ⅱ)存在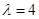 ,使得对任意的
,使得对任意的 ,都有
,都有 成立,证明如下:
成立,证明如下:
证法1:记直线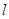 与x轴的交点为
与x轴的交点为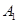 ,则
,则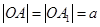 。于是有
。于是有
 ………8分
………8分
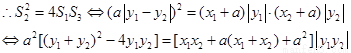 ………10分
………10分
将①、②、③代入上式化简可得
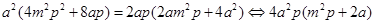
上式恒成立,即对任意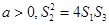 成立
……………12分
成立
……………12分
证法2:如图2,连接 ,则由
,则由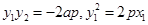 可得
可得
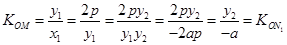 ,
,
所以直线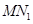 经过原点O,同理可证直线
经过原点O,同理可证直线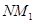 也经过原点O ……………9分
也经过原点O ……………9分
又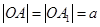 设
设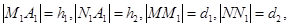
则  …………12分
…………12分

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 (2012•大丰市一模)如图所示,已知平面直角坐标系xOy,抛物线y=-x2+bx+c过点A(4,0)、B(1,3).
(2012•大丰市一模)如图所示,已知平面直角坐标系xOy,抛物线y=-x2+bx+c过点A(4,0)、B(1,3).