题目内容

如图，平行四边形ABCD中，点E是边BC（靠近点B）的三等分点，F是AB（靠近点A）的三等分点，P是AE与DF的交点，则
AP
用
AB
，
AD
表示为
AP
=
3
10
AB
+
1
10
AD
AP
=
3
10
AB
+
1
10
AD
．
分析：设
AP
=λ
AE
，将
AP
表示为
AB
、
AD
一个线性组合，再设
DP
=μ
DF
，得到
AP
关于
AB
、
AD
的另一个线性组合，根据平面向量基本定理建立关于λ、μ的方程组并解之得λ的值，从而得到
AP
=
3
10
AB
+
1
10
AD
．
解答：解：设
AP
=λ
AE
，而
AE
=
AB
+
BE
=
AB
+
1
3
BC

∴
AP
=λ
AB
+
1
3
λ
BC
=λ
AB
+
1
3
λ
AD
…①
再设
DP
=μ
DF
=
1
3
μ
AB
-μ
AD

∴
AP
=
AD
+
DP
=
1
3
μ
AB
+（1-μ）
AD
…②
比较①②，得λ=
1
3
μ且
1
3
λ=1-μ，解之得λ=
3
10

将λ=
3
10
代入①，得
AP
=
3
10
AB
+
1
10
AD

故答案为：
AP
=
3
10
AB
+
1
10
AD
点评：本题给出平行四边形ABCD一组邻边的两个三等分点，求一个向量表示为
AB
、
AD
的线性组合，着重考查了平行四边形的性质、平面向量加减法则和平面向量基本定理等知识点，属于基础题．
练习册系列答案
相关题目
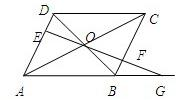精英家教网如图，平行四边形ABCD的对角线交于点O，过点O的直线交AD于E，BC于F，交AB延长线于G，已知AB=a，BC=b，BG=c，则BF=
 
．
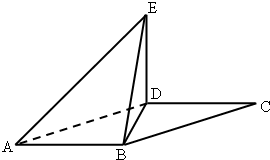精英家教网如图，平行四边形ABCD中，∠DAB=60°，AB=2，AD=4将△CBD沿BD折起到△EBD的位置，使平面EDB⊥平面ABD．
（I）求证：AB⊥DE
（Ⅱ）求三棱锥E-ABD的侧面积．
如图，平行四边形ABCD中，E，F分别是BC，DC的中点，G为交点，若
AB
=
a
，
AD
=
b
，试以
a
，
b
为基底表示
CG
=
-
1
3
(
a
+
b
)
-
1
3
(
a
+
b
)
．
（2012•枣庄一模）如图，平行四边形ABCD中，点E是边BC（靠近点B）的三等分点，F是AB（靠近点A）的三等分点，P是AE与DF的交点，则
AP
用
AB
，
AD
表示为
AP
=
3
10
AB
+
1
10
AD
AP
=
3
10
AB
+
1
10
AD
．
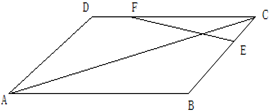精英家教网如图，平行四边形ABCD中，
AB
=
a
，
AD
=
b
，
CE
=
1
3
CB
，
CF
=
2
3
CD
．
（1）用
a
，
b
表示
EF
；
（2）若|
a
|=1，|
b
|=4，∠DAB=60°，分别求|
EF
|和
AC
•
FE
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网