题目内容
函数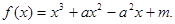
(1)若函数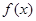 在
在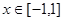 内没有极值点,求
内没有极值点,求 的取值范围;
的取值范围;
(2)若对任意的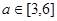 ,不等式
,不等式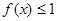 在
在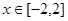 上恒成立,求实数
上恒成立,求实数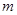 的取值范围.
的取值范围.
(1) 或
或 或
或 ;(2)
;(2) .
.
解析试题分析:(1)要使函数f(x)在x∈[-1,1]内没有极值点,只需f′(x)=0在[-1,1]上没有实根即可,即f′(x)=0的两根x=-a或x= 不在区间[-1,1]上;(2)求导函数,来确定极值点,利用a的取值范围,求出f(x)在x∈[-2,2]上的最大值,再求满足f(x)≤1时m的取值范围.
不在区间[-1,1]上;(2)求导函数,来确定极值点,利用a的取值范围,求出f(x)在x∈[-2,2]上的最大值,再求满足f(x)≤1时m的取值范围.
解:(1)由题意知, ,当
,当 时,合题意,当
时,合题意,当 时,因为
时,因为 ,所以
,所以 ,解得
,解得 或
或 ,综上
,综上 或
或 或
或 .
.
(2) ,又
,又 ,所以函数
,所以函数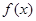 的递增区间为
的递增区间为 ,递减区间为
,递减区间为 .当
.当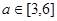 时,
时, ,所以
,所以 ,而
,而 ,所以
,所以 ,因为
,因为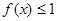 在
在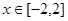 上恒成立,所以
上恒成立,所以 ,即
,即 在
在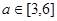 上恒成立,所以
上恒成立,所以 .
.
考点:利用导数求闭区间上函数的最值;利用导数研究函数的极值.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
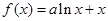 ,对任意的
,对任意的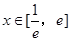 时,
时,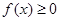 恒成立,则a的范围为 .
恒成立,则a的范围为 . ,若函数
,若函数 有大于零的极值点,则
有大于零的极值点,则 的取值范围是________.
的取值范围是________.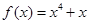 图像上一点,在A处的切线平行于直线
图像上一点,在A处的切线平行于直线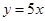 ,则A点坐标为 ;
,则A点坐标为 ; 是函数
是函数 的导数,则
的导数,则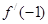 =
= 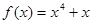 图像上一点,在A处的切线平行于直线
图像上一点,在A处的切线平行于直线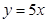 ,则A点坐标为 ;
,则A点坐标为 ; 的图象与
的图象与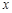 轴所围成的封闭图形的面积等于_______.
轴所围成的封闭图形的面积等于_______. ,g(x)=
,g(x)= -m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.
-m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________. .若曲线
.若曲线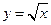 与直线
与直线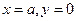 所围成封闭图形的面积为
所围成封闭图形的面积为 ,则
,则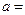 ______.
______.