题目内容
函数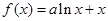 ,对任意的
,对任意的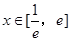 时,
时,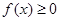 恒成立,则a的范围为 .
恒成立,则a的范围为 .
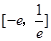
解析试题分析:对任意的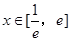 时,
时,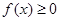 恒成立,即只需
恒成立,即只需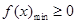 即可。
即可。
当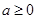 时在
时在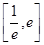 上
上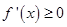 恒成立,即
恒成立,即 在
在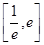 上单调递增。所以
上单调递增。所以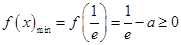 ,解得
,解得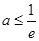 。又因为
。又因为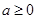 ,所以
,所以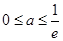 。
。
当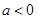 时,令
时,令 得
得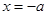
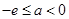
①当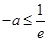 即
即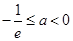 时,在
时,在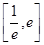 上
上 恒成立,所以
恒成立,所以 在
在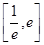 上单调递增。所以
上单调递增。所以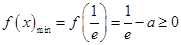 ,解得
,解得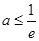 。又因为
。又因为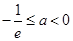 ,所以
,所以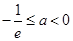 。
。
②当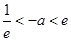 即
即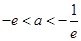 时,令
时,令 得
得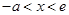 。令
。令 得
得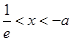 ,所以
,所以 在
在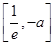 上单调递减,在
上单调递减,在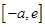 上单调递增。所以
上单调递增。所以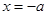 时
时 取得最小值。此时
取得最小值。此时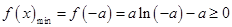 ,解得,又因为
,解得,又因为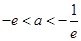 ,所以
,所以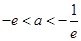 。
。
③当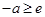 即
即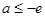 时,在
时,在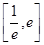 上
上 ,所以
,所以 在
在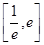 上单调递减,所以
上单调递减,所以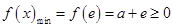 ,解得
,解得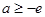 ,因为
,因为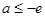 ,所以
,所以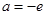 。
。
综上可得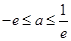 。
。
考点:用导数研究函数的单调性及最值。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
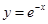 上点
上点 处的切线平行于直线
处的切线平行于直线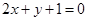 ,则点
,则点 在区间
在区间 上是单调递增函数,则实数
上是单调递增函数,则实数 的取值范围是 .
的取值范围是 . (用数字作答).
(用数字作答).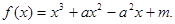
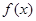 在
在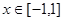 内没有极值点,求
内没有极值点,求 的取值范围;
的取值范围;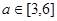 ,不等式
,不等式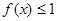 在
在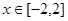 上恒成立,求实数
上恒成立,求实数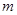 的取值范围.
的取值范围.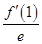 ·ex-f(0)x+
·ex-f(0)x+ x2在点(1,f(1))处的切线方程为____________.
x2在点(1,f(1))处的切线方程为____________.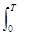 x2dx=9,则常数T的值为________.
x2dx=9,则常数T的值为________.