题目内容
在△ABC中，若B＝60°，2b＝a＋c，则△ABC的形状是（ ）
A.等腰直角三角形
B.直角三角形
C.
D.
D 解析一：根据余弦定理得b2＝a2＋c2－2accos B.
∵ B＝60°，2b＝a＋c，
∴ (
)2＝a2＋c2－2accos 60°，
整理得(a－c)2＝0
，∴ a＝c.∴ △ABC是等边三角形．
解析二：根据正弦定理得，
2b＝a＋c可转化为2sin B＝sin A＋sin C.
又∵ B＝60°，∴ A＋C＝120°，∴ C＝120°－A，
∴ 2sin 60°＝sin A＋sin(120°－A)，整理得sin(A＋30°)＝1，
∴ A＝60°，C＝60°.∴ △ABC是等边三角形．
练习册系列答案
相关题目
，
，则a＝________．
，AB＝2
，AC＝2，则△ABC的面积是_____.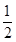
，
，
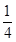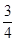] D．[－