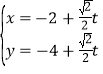题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() .数列
.数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求正整数
,求正整数![]() 的值;
的值;
(2)若数列![]() ,
,![]() 均是等差数列,求
均是等差数列,求![]() 的取值范围;
的取值范围;
(3)若数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,且
,且![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差数列,若存在,求出一个
成等差数列,若存在,求出一个![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)2;(2)![]() ;(3)存在,k=1.
;(3)存在,k=1.
【解析】
(1)在原式中令n=m,代入![]() ,即可解出m;(2)设出数列
,即可解出m;(2)设出数列![]() ,
,![]() 的首项和公差,代入原式化简得一个含n的恒等式,所以对应系数相等得到
的首项和公差,代入原式化简得一个含n的恒等式,所以对应系数相等得到![]() ;(3)当
;(3)当![]() 时,
时,![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
解:(1)因为![]() ,且
,且![]()
所以![]()
解得![]()
(2)记数列![]() ,首项为
,首项为![]() ,公差为
,公差为![]() ;数列
;数列![]() ,首项为
,首项为![]() ,公差为
,公差为![]()
则![]() ,
,
化简得:![]()
所以![]()
所以![]() 的取值范围
的取值范围![]()
(3)当![]() 时,
时,![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
下面论证当![]() 时,
时,![]() ,
,![]() ,
,![]() 不成等差数列
不成等差数列
因为![]() ,所以
,所以![]()
所以![]() ,所以
,所以![]()
所以![]()
若![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]()
所以![]() ,所以
,所以![]() ,解得
,解得![]()
当![]() 时,
时,![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]()
因为![]()
所以![]()
所以当![]() 时,
时,![]() ,
,![]() ,
,![]() 不成等差数列
不成等差数列
综上所述:存在且仅存在正整数![]() 时,
时,![]() ,
,![]() ,
,![]() 成等差数列
成等差数列

练习册系列答案
相关题目
【题目】(1)某校夏令营有3名男同学A、B、C和3名女同学X、Y、Z,其年级情况如下表:
一年级 | 二年级 | 三年级 | |
男同学 | A | B | C |
女同学 | X | Y | Z |
现从这6名同学中随机选出2人参加知识竞赛(每人被选到的可能性相同).
①用表中字母列举出所有可能的结果;
②设M为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件M发生的概率.
(2)节日前夕,小李在家门前的树上挂了两串彩灯.这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮.那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是多少?