题目内容
求证:点P(x0,y0)到直线Ax+By+C=0的距离d=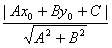 .
.
证明:设Q(x,y)是直线上任意一点,则Ax+By+C=0.
因为|PQ|2=(x-x0)2+(y-y0)2,A2+B2≠0,由柯西不等式,得
(A2+B2)[(x-x0)2+(y-y0)2]≥[A(x-x0)+B(y-y0)]2=[(Ax+By)-(Ax0+By0)]2=(Ax0+By0+C)2,
所以|PQ|≥![]() ,
,
当![]() 时,取等号,
时,取等号,
由垂线段最短得d=![]() .
.

练习册系列答案
相关题目
题目内容
求证:点P(x0,y0)到直线Ax+By+C=0的距离d=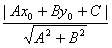 .
.
证明:设Q(x,y)是直线上任意一点,则Ax+By+C=0.
因为|PQ|2=(x-x0)2+(y-y0)2,A2+B2≠0,由柯西不等式,得
(A2+B2)[(x-x0)2+(y-y0)2]≥[A(x-x0)+B(y-y0)]2=[(Ax+By)-(Ax0+By0)]2=(Ax0+By0+C)2,
所以|PQ|≥![]() ,
,
当![]() 时,取等号,
时,取等号,
由垂线段最短得d=![]() .
.
