题目内容

已知△ABC中，AC=1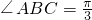， $数学公式$ ，D为BC中点，则△ABD的最大面积是________．

$\text{[math]}$
分析：利用余弦定理通过基本不等式求出ac的最大值，然后利用D为BC中点，则△ABD的最大面积．
解答：因为D为BC中点，则△ABD的面积是三角形ABC面积的一半，
由余弦定理可知1=a²+c²-2accos60°，
即1=a²+c²-ac≥2ac-ac=ac，所以ac≤1，当且仅当a=c时等号成立．
S_△ABD= $\text{[math]}$ S_△ABC= $\text{[math]}$ ≤ $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：本题是中档题，考查余弦定理的应用，三角形的面积求法，考查计算能力．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

已知△ABC中，AC=1，∠ABC=

，设∠BAC=x，记f（x）=AB．
（Ⅰ）求f（x）的解析式及定义域；
（Ⅱ）D是AB边的中点，若f(x)=

（2010•闵行区二模）已知△ABC中，AC=2

，BC=2，则角A的取值范围是（　　）

已知△ABC中，AC=BC=2，∠ACB=120°，D为AB的中点，E，F分别在线段AC，BC上，且EF∥AB，EF交CD于G，把△ADC沿CD折起，如图所示，

（1）求证：E₁F∥平面A₁BD；
（2）当二面角A₁-CD-B为直二面角时，是否存在点F，使得直线A₁F与平面BCD所成的角为60°，若存在求CF的长，若不存在说明理由．

已知△ABC中，AC=1，∠ABC=

．设∠BAC=x，记f（x）=AB．
（Ⅰ）求f（x）的解析式及定义域；
（Ⅱ）设g（x）=6m•f（x）+1，求实数m，使函数g（x）的值域为（1，

（2010•抚州模拟）已知△ABC中，AC=1，∠ABC=

，设∠BAC=x，并记f(x)=

．
（1）求函数f（x）的解析式及其定义域；
（2）设函数g（x）=6mf（x）+1，若函数g（x）的值域为(1，

]，试求正实数m的值．