题目内容

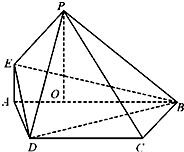
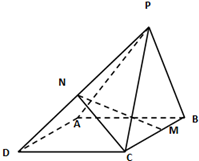
如图，P是二面角α-AB-β棱AB上的一点，分别在α，β上引射线PM，PN，如果∠BPM=∠BPN=45°，∠MPN=60°，那么二面角α-AB-β的大小是 ______．
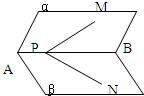
过AB上一点Q分别在α，β内做AB的垂线，交PM，PN于M点和N点
则∠MQN即为二面角α-AB-β的平面角，如下图所示：
设PQ=a，则∵∠BPM=∠BPN=45°
∴QM=QN=a
PM=PN=
2
a
又由∠MPN=60°，易得△PMN为等边三角形
则MN=
2
a
解三角形QMN易得∠MQN=90°
故答案为：90°
练习册系列答案
相关题目
如图，已知PO⊥平面ABCD，点O在AB上，EA∥PO，四边形ABCD是直角梯形，AB∥DC，且BC⊥AB，BC=CD=BO=PO，EA=AO=
1
2
CD．
（Ⅰ）求证：PE⊥平面PBC；
（Ⅱ）求二面角C-PB-D的大小；
（Ⅲ）在线段PE上是否存在一点M，使DM∥平面PBC，若存在求出点M；若不存在，说明理由．
已知正三棱柱ABC-A1B1C1的底面边长为2，高为1，过顶点A作一平面α与侧面BCC1B1交于EF，且EF∥BC．若平面α与底面ABC所成二面角的大小为x(0＜x≤
π
6
)，四边形BCEF面积为y，则函数y=f（x）的图象大致是（　　）
A．B．C．D．
正三棱锥的高为
3
，侧棱长为
7
，那么侧面与底面所成二面角的大小是（　　）
A．60°B．30°C．arccos
21
7
D．arcsin
21
7
在二面角α-l-β中，A∈l，B∈l，AC?α，BD?β，且AC⊥l，BD⊥l，已知AB=1，AC=BD=2，CD=
5
，则二面角α-l-β的余弦值为______．
在三棱锥S-ABC中，如图，∠SAB=∠SAC=∠ACB=90°，AC=2，
BC=
13
，SB=
29
．
（1）证明：SC⊥BC；
（2）求侧面SBC与底面ABC所成的二面角大小；
（3）（理）求异面直线SC与AB所成的角的大小（用反三角函数表示）．
（文）求三棱锥的体积VS-ABC．
如图所示，在四棱锥P-ABCD中，四边形ABCD为菱形，∠ABC=60°，AB=2，△PCB为正三角形，且平面PCB⊥平面ABCD，M，N分别为BC，PD的中点．
（1）求证：MN∥面APB；
（2）求二面角B-NC-P的余弦值；
（3）求四棱锥P-ABCD被截面MNC分成的上下两部分体积之比．
如图，边长为2的正方形ABCD中，点E、F分别是边AB、BC上的点，将△AED、△DCF分别沿DE、DF折起，使A、C两点重合于点A′．
（1）△A′EF恰好是正三角形且Q是A′F的中点，求证：EQ⊥平面A′FD
（2）当E、F分别是AB、BC的中点时，求二面角A′-EF-D的正弦值．
已知两条互不重合的直线m，n，两个不同的平面α，β，下列命题中正确的是(  )
A．若m∥α，n∥β，且m∥n，则α∥β
B．若m⊥α，n∥β，且m⊥n，则α⊥β
C．若m⊥α，n∥β，且m∥n，则α∥β
D．若m⊥α，n⊥β，且m⊥n，则α⊥β

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网