题目内容
8．在极坐标系中，求以点A（1，0）为圆心，且过点B（2，$\frac{π}{3}$）的圆的极坐标方程．分析 设圆的极坐标方程为ρ2-2ρcosθ-m=0，由圆过点B（2，$\frac{π}{3}$），求出m，由此能求出圆的极坐标方程．
解答 解：因为点A（1，0）为圆心，
所以可设圆的极坐标方程为ρ2-2ρcosθ-m=0，
又因为圆过点B（2，$\frac{π}{3}$），所以4-2-m=0，即m=2，
所以圆的极坐标方程为ρ2-2ρcosθ-2=0．…（10分）
点评 本题考查圆的极坐标方程的求法，是基础题，解题时要认真审题，注意直角坐标和极坐标互化公式的合理运用．
练习册系列答案
相关题目
18．如图，在正方体ABCD-A1B1C1D1中，若M是线段A1C1上的动点，则下列结论不正确的是（ ）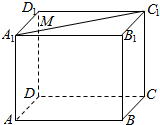
| A． | 三棱锥M-ABD的主视图面积不变 | B． | 三棱锥M-ABD的侧视图面积不变 | ||
| C． | 异面直线CM，BD所成的角恒为$\frac{π}{2}$ | D． | 异面直线CM，AB所成的角可为$\frac{π}{4}$ |
