Question

1．已知|$\overrightarrow{OA}$|=$\sqrt{3}$，|$\overrightarrow{OB}$|=3，$\overrightarrow{OA}$•$\overrightarrow{OB}$=0，点C在∠AOB内，且∠AOC=30°，设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$（m，n∈R），则$\frac{m}{n}$等于（　　）

• A． $\frac{1}{3}$
• B． 3
• C． $\frac{\sqrt{3}}{3}$
• D． $\sqrt{3}$

Answer 1

分析 将向量$\overrightarrow{OC}$分解到$\overrightarrow{OA}$，$\overrightarrow{OB}$，可得$\overrightarrow{OC}$=$\overrightarrow{OD}$+$\overrightarrow{OE}$，由解直角三角形知识和向量共线定理，可得m，n，即可得到所求值．

解答 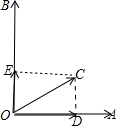解：如图所示，将向量$\overrightarrow{OC}$分解到$\overrightarrow{OA}$，$\overrightarrow{OB}$，
可得$\overrightarrow{OC}$=$\overrightarrow{OD}$+$\overrightarrow{OE}$，
由|$\overrightarrow{OD}$|=|$\overrightarrow{OC}$|cos30°=$\frac{\sqrt{3}}{2}$|$\overrightarrow{OC}$|，
|$\overrightarrow{OE}$|=|$\overrightarrow{OC}$|sin30°=$\frac{1}{2}$|$\overrightarrow{OC}$|，
则m=$\frac{\frac{\sqrt{3}}{2}}{\sqrt{3}}$=$\frac{1}{2}$，n=$\frac{\frac{1}{2}}{3}$=$\frac{1}{6}$，
即有$\frac{m}{n}$=3．
故选：B．

点评 本题考查向量垂直的条件：数量积为0，考查向量的分解，以及向量共线定理的运用，属于基础题．