题目内容
12.设计一个算法,计算1+3+5+…+2011的值,并画出程序框图.分析 由已知中程序的功能为用循环结构计算1+3+5+…+2011的值,为累加运算,可令循环变量的初值为1,终值为2011,步长为2,由此确定循环前和循环体中各语句,即可得到相应的程序框图.
解答 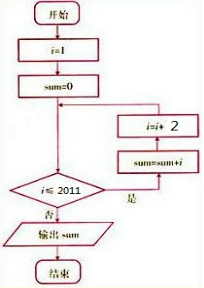 解:第一步:设i的值为1;
解:第一步:设i的值为1;
第二步:设sum的值为0;
第三步:如果i≤2011执行第四步,
否则转去执行第七步;
第四步:计算sum+i并将结果代替sum;
第五步:计算i+2并将结果代替i;
第六步:转去执行第三步;
第七步:输出sum的值并结束算法.
点评 本题考查的知识点是设计程序框图解决实际问题,其中熟练掌握利用循环进行累加和累乘运算的方法,是解答本题的关键.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
2.已知a>0且a≠1,则使关于x的方程loga(x-2ak)=loga(x2-a2)有解的k的取值范围是( )
| A. | 0<k<$\frac{1}{2}$或k$<-\frac{1}{2}$ | B. | 0<k<1或k<-1 | C. | 0<k<2或k<-2 | D. | 0<k<1或k<-2 |
20.函数y=f(x)(x∈(0,3))图象如图所示,若0<x1<x2<3,则有( )


| A. | $\frac{f({x}_{1})}{{x}_{1}}$<$\frac{f({x}_{2})}{{x}_{2}}$ | B. | $\frac{f({x}_{1})}{{x}_{1}}$=$\frac{f({x}_{2})}{{x}_{2}}$ | ||
| C. | $\frac{f({x}_{1})}{{x}_{1}}$>$\frac{f({x}_{2})}{{x}_{2}}$ | D. | 前三个判断都不正确 |
