题目内容
已知函数f(x)满足f(x+y)=f(x)•f(y),且 .
.
(Ⅰ)当x=n,y=1,n∈N*时,求f(n)的表达式:
(Ⅱ)设an=n•f(n)(n∈N*),求证:a1+a2+…+an<2
解:(I)x=n,y=1得: .
.
∴数列{f(n)}是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.
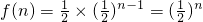 .(4分)
.(4分)
(Ⅱ)设Tn=a1+a2++an
∵ (n∈N*).
(n∈N*).
∴
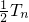
=
两式相减得:
= .
.
∴ .(10分)
.(10分)
分析:(I)x=n,y=1得: .则由等比数列的定义知,数列{f(n)}是以
.则由等比数列的定义知,数列{f(n)}是以 为首项,
为首项, 为公比的等比数列.(Ⅱ)设Tn=a1+a2+…+an其通项公式是
为公比的等比数列.(Ⅱ)设Tn=a1+a2+…+an其通项公式是 是一个等差数列和等比数列对应项积的形式,则由错位相减法求得前n项和,再用放缩法证明不等式.
是一个等差数列和等比数列对应项积的形式,则由错位相减法求得前n项和,再用放缩法证明不等式.
点评:本题主要考查抽象函数求解析式,进而转化为数列研究数列的通项及用错位相减法求前n项和.
 .
.∴数列{f(n)}是以
 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.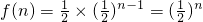 .(4分)
.(4分)(Ⅱ)设Tn=a1+a2++an
∵
 (n∈N*).
(n∈N*).∴

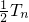
=

两式相减得:

=
 .
.∴
 .(10分)
.(10分)分析:(I)x=n,y=1得:
 .则由等比数列的定义知,数列{f(n)}是以
.则由等比数列的定义知,数列{f(n)}是以 为首项,
为首项, 为公比的等比数列.(Ⅱ)设Tn=a1+a2+…+an其通项公式是
为公比的等比数列.(Ⅱ)设Tn=a1+a2+…+an其通项公式是 是一个等差数列和等比数列对应项积的形式,则由错位相减法求得前n项和,再用放缩法证明不等式.
是一个等差数列和等比数列对应项积的形式,则由错位相减法求得前n项和,再用放缩法证明不等式.点评:本题主要考查抽象函数求解析式,进而转化为数列研究数列的通项及用错位相减法求前n项和.

练习册系列答案
相关题目