题目内容
(1)求证:如果一个平面经过一条线段的中点,那么这条线段的两个端点到平面的距篱相等;
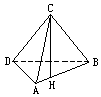
(2)求证:空间四边形的两条对角线到这空间四边形各边中点所在平面的距离相等.
答案:
解析:
解析:
|
证明 (1)如图,O是线段AB的中点,且O∈平面α.
作 进而可以知道,若AB,AC,AD是空间不共面的三条线段,则A,B,C,D四点到线段AB,AC,AD的中点确定的平面的距离相等. (2)如图,设E,F,G,H依次是空间四边形ABCD的边AB,BC,CD,DA的中点,我们已证明E,F,G,H四点共面.
∵EF和EH分别是△ABC和△ABD的中位线, ∴AC∥EF,BD∥EH. ∵AC,BD都在平面EFGH外, ∴AC∥平面EFGH,BD∥平面EFGH. A到平面EFGH的距离就是AC到平面EFGH的距离,B到平面EFGH的距离就是BD到平面EFGH的距离. ∵平面EFGH经过AB的中点E,∴A,B到平面EFGH的距离相等. 故AC,BD到平面EFGH的距离也相等. 进而可以得到A,B,C,D到平面EFGH的距离也相等. 求距离是立体几何中一类重要的计算问题,在求解这类计算题时一般需要有三个步骤: (1)作图:即作出长度表示距离的线段; (2)证明:即证明所作线段的长就是所求的距离; (3)计算:根据已知条件计算出所作线段的长度得出所求的距离. |

练习册系列答案
相关题目

 ⊥α,
⊥α, ⊥α,
⊥α, 为垂足,则
为垂足,则 分别是A,B到平面α的距离,且
分别是A,B到平面α的距离,且 确定平面β,β∩α=
确定平面β,β∩α= .∵O∈AB,AB
.∵O∈AB,AB β,∴O∈β;又O∈α,∴O∈
β,∴O∈β;又O∈α,∴O∈ .∵
.∵ ⊥α,
⊥α, ⊥α,∴
⊥α,∴ ⊥
⊥ ,∵∠
,∵∠ =∠
=∠ =
= ,
, ,AO=BO,∴△
,AO=BO,∴△ ,∴
,∴ ,即线段AB的两个端点到平面α的距离相等.
,即线段AB的两个端点到平面α的距离相等.
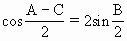 ;
;
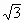 ,试求二面角C-AD-B的正弦值.
,试求二面角C-AD-B的正弦值. (n∈N*)上的最小值为bx令an=ln(1+n)-bx。
(n∈N*)上的最小值为bx令an=ln(1+n)-bx。 恒成立,求实数c的取值范围;
恒成立,求实数c的取值范围; 。
。