题目内容
设ABCD是矩形，沿对角线BD将△BDC折起，使C点在底面DAB内的射影H恰好落在AB边上(如图)．
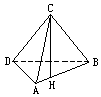
(1)求证：平面ABC⊥平面ACD；
(2)求证：平面DBC⊥平面ACD；
(3)如果AD∶AB＝1∶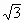
，试求二面角C－AD－B的正弦值．
答案：
解析：
解析：
|
(1)AB为直线BC在平面ABD内的射影，而AD⊥AB(已知)，由三垂线定理，得AD⊥BC，又由已知有BC⊥CD， ∴BC⊥平面ACD，BC ∴面ABC⊥面ACD． (2)BC (3)AH为AC在平面ACD的射影，又AH⊥AD ∴AC⊥AD． 从而∠CAH为二面角C－AD－B的平面角． 设AD＝a，AB＝ 在Rt△ACD中，AC＝ ∴BC⊥AC ∴sin∠CAH＝ |
平面ABC．
a，则DC＝
，又BC⊥平面ACD
＝
＝
．
练习册系列答案
阅读快车系列答案
相关题目
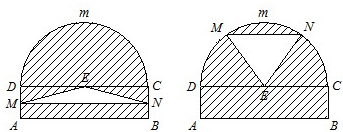（2009•普陀区二模）某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是矩形，其中AB=2米，BC=0.5米．上部CmD是个半圆，固定点E为CD的中点．△EMN是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆（MN和AB、DC不重合）．
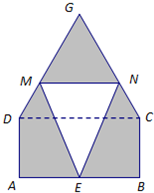（2013•静安区一模）某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是矩形，其中AB=2米，BC=1米；上部CDG是等边三角形，固定点E为AB的中点．△EMN是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆．
某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是矩形，其中AB=2米，BC=1米；上部CDG是等边三角形，固定点E为AB的中点．△EMN是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆．