题目内容
曲线C1的参数方程为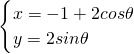
（θ为参数，曲线C2的极坐标方程为ρ=2，以极点为原点．极轴为x轴的非负半轴，则曲线C1与C2的公共弦所在直线的直角坐标系方程为 ________．
x=-
分析：把两个曲线的参数方程和极坐标方程分别化为普通方程，发现他们表示的曲线都是圆，将两圆的方程相减即得公共弦所在的直线方程．
解答：曲线C1的普通方程为 （x+1）2+y2=4，表示以（-1，0）为圆心、以2为半径的圆，
曲线C2的普通方程为 x2+y2=4，
将两圆的方程相减可得公共弦所在的直线方程为2x+1=0，即x=-，
故答案为x=-．
点评：本题考查把曲线的参数方程或极坐标方程化为普通方程的方法，以及两圆的公共弦所在的直线方程的求法．
分析：把两个曲线的参数方程和极坐标方程分别化为普通方程，发现他们表示的曲线都是圆，将两圆的方程相减即得公共弦所在的直线方程．
解答：曲线C1的普通方程为 （x+1）2+y2=4，表示以（-1，0）为圆心、以2为半径的圆，
曲线C2的普通方程为 x2+y2=4，
将两圆的方程相减可得公共弦所在的直线方程为2x+1=0，即x=-
，故答案为x=-
．点评：本题考查把曲线的参数方程或极坐标方程化为普通方程的方法，以及两圆的公共弦所在的直线方程的求法．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目