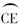题目内容
如图2-4-12,P为⊙O的直径CB延长线上的一点,A为⊙O上一点,若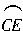
图2-4-12
(1)求证:PA为⊙O的切线;
(2)若∠BEA =30°,BD =1,求AP及PB的长.
思路分析:对于(1),A已经是圆上一点,所以可以连结OA,证明PA与OA垂直;对于(2),将∠E利用圆周角定理转移到Rt△ODA和Rt△OAP中,解直角三角形即可得到线段AP及PB的长.

(1)证明:连结AO,∵![]() =
=![]() ,BC为直径,∴AE⊥BC,AD =DE,
,BC为直径,∴AE⊥BC,AD =DE, ![]() =
=![]() .
.
∵OA =OB,∴∠C =∠3.?
∴∠1=2∠C.?
又∵∠C =![]() ∠PAD,∴∠1=∠2.?
∠PAD,∴∠1=∠2.?
∵∠1+∠4=90°,?
∴∠2+∠4=90°.?
∴PA⊥OA.?
∴PA为⊙O的切线.
(2)解:在Rt△EBD中,∵∠BEA =30°,BD=1,∴BE =2,DE =![]() .?
.?
在Rt△ODA和Rt△EBD中,∠4=90°-∠1=90°-2∠C=90°-2∠E =30°=∠E,∠ODA =∠BDE,?AD =ED,?
∴Rt△ODA≌Rt△EBD.?
∴AD =DE =![]() ,OD =BD =1,OA =BE =2.?
,OD =BD =1,OA =BE =2.?
在Rt△OAP中,∵AD⊥OP,?
∴AD2=OD·DP,即![]() =1·DP.?
=1·DP.?
∴DP =3.?
∴BP =2.?
在Rt△ADP中,根据勾股定理,得![]() =
=![]() =
=![]() .
.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
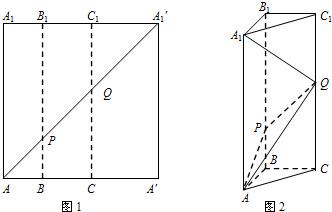 如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
如图1所示,在边长为12的正方形AA′A1′A1中,点B,C在线段AA′上,且AB=3,BC=4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P,作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q,将该正方形沿BB1、CC1折叠,使得A′A1′与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.