题目内容
已知向量 =(2cos2x,
=(2cos2x, ),
), =(1,sin2x),函数
=(1,sin2x),函数 .
.
(1)求函数f(x)的最小正周期和单调增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,R为△ABC外接圆的半径,且f(C)=3,c=1, ,且a>b,求a,b的值.
,且a>b,求a,b的值.
解:(1)由题意可得 =
=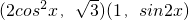
= =
= =
=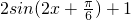 ,
,
∴f(x)的最小正周期为π,由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ (k∈Z),
(k∈Z),
解得kπ
 (k∈Z)
(k∈Z)
∴函数f(x)的单调增区间为(k ,kπ
,kπ )(k∈Z)
)(k∈Z)
(2)由(1)知 ∴
∴
∵C是三角形内角,∴ ,
,
∴ ,即:
,即: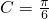
由余弦定理可得: 即:
即: ①
①
由正弦定理可得: 可得:
可得: ②,联立①②得:
②,联立①②得:
解之得:a2=3或4,∴a=
所以当 时,b=2; 当a=2,
时,b=2; 当a=2, ,∵a>b,∴a=2,
,∵a>b,∴a=2,
分析:(1)由题意结合数量积的定义可得函数f(x),由周期公式和整体代入可得答案;
(2)由(1)结合f(C)=3可得角C的值,然后又余弦定理和正弦定理可得关于a,b的方程,联立可解,再由a>b可做取舍.
点评:本题为向量和三角函数以及解三角形的结合,熟练利用公式进行运算是解决问题的关键,属中档题.
 =
=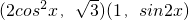
=
 =
= =
=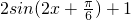 ,
,∴f(x)的最小正周期为π,由2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ (k∈Z),
(k∈Z),解得kπ

 (k∈Z)
(k∈Z)∴函数f(x)的单调增区间为(k
 ,kπ
,kπ )(k∈Z)
)(k∈Z) (2)由(1)知
 ∴
∴
∵C是三角形内角,∴
 ,
,∴
 ,即:
,即: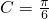
由余弦定理可得:
 即:
即: ①
①由正弦定理可得:
 可得:
可得: ②,联立①②得:
②,联立①②得:
解之得:a2=3或4,∴a=

所以当
 时,b=2; 当a=2,
时,b=2; 当a=2, ,∵a>b,∴a=2,
,∵a>b,∴a=2,
分析:(1)由题意结合数量积的定义可得函数f(x),由周期公式和整体代入可得答案;
(2)由(1)结合f(C)=3可得角C的值,然后又余弦定理和正弦定理可得关于a,b的方程,联立可解,再由a>b可做取舍.
点评:本题为向量和三角函数以及解三角形的结合,熟练利用公式进行运算是解决问题的关键,属中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目