题目内容
已知曲线
（t为参数），则圆心为 ________，半径为 ________．
（-4，3） 1
分析：先利用sin2t+cos2t=1消去参数t，即可将参数方程化成直角坐标方程，然后根据圆的标准方程求出圆心和半径即可．
解答：曲线（t为参数），
∵sin2t+cos2t=1
∴圆的直角坐标方程为（x+4）2+（x-3）2=1
∴圆心为（-4，3），半径为1．
故答案为（-4，3），1
点评：本题主要考查了圆的参数方程，圆的参数方程化成直角坐标方程常常利用sin2t+cos2t=1进行消参，属于基础题．
分析：先利用sin2t+cos2t=1消去参数t，即可将参数方程化成直角坐标方程，然后根据圆的标准方程求出圆心和半径即可．
解答：曲线
（t为参数），∵sin2t+cos2t=1
∴圆的直角坐标方程为（x+4）2+（x-3）2=1
∴圆心为（-4，3），半径为1．
故答案为（-4，3），1
点评：本题主要考查了圆的参数方程，圆的参数方程化成直角坐标方程常常利用sin2t+cos2t=1进行消参，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
：
(t为参数)与曲线
：
(
为参数，
) 有一个公共点在X轴上，则
.
：
(t为参数)与曲线
：
(
为参数，
) 有一个公共点在X轴上，则
.
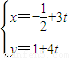（t为参数）与曲线
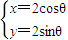（θ为参数）的交点为A，B，，则|AB|= ．
（t为参数），
，C
的方程为普通方程，并说明它们分别表示什么曲线；
，Q为C
中点
到直线
（t为参数）距离的最小值。
：
(t为参数)与曲线
：
(
为参数，
) 有一个公共点在X轴上，则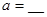
.