题目内容
已知P是△ABC所在平面内一点,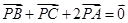 ,现将一粒红豆随机撒在△ABC内,则红豆落在△PBC内的概率是( )
,现将一粒红豆随机撒在△ABC内,则红豆落在△PBC内的概率是( )
A.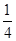 B.
B.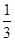 C.
C.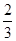 D.
D.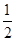
【答案】
D
【解析】
试题分析:以PB、PC为邻边作平行四边形PBDC,

则 ,
,
∵ ,
,
∴ ,得
,得 ,
,
由此可得,P是△ABC边BC上的中线AO的中点,
点P到BC的距离等于A到BC的距离的 .
.
∴S△PBC= S△ABC.
S△ABC.
将一粒黄豆随机撒在△ABC内,黄豆落在△PBC内的概率为P= ,
,
故选D.
考点:平面向量的线性运算,几何概型概率的计算。
点评:中档题,确定三角形面积关系是解题的关键。

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
已知P是△ABC所在平面内一点,
+
+2
=
,现将一粒黄豆随机撒在△ABC内,则黄豆落在△APC内的概率是( )
| PB |
| PC |
| PA |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知P是△ABC所在平面内的一点,若
-
=λ
,其中λ∈R,则点P一定在( )
| CB |
| PB |
| PA |
| A、AC边所在的直线上 |
| B、BC边所在的直线上 |
| C、AB边所在的直线上 |
| D、△ABC的内部 |