Question

设a∈R,f(x)为奇函数,且.?

(1)试求f(x)的反函数f ^-1 (x)及其定义域;?

(2)设g(x)=,若x∈［,］时,f ^-1(x)≤g(x)?恒成立,试求实数k的范围.

Answer 1

解析：（1）由题意知，

 

∵f(x)为奇函数，?

∴f(-x)=-f(x),?

化简有(2^x+1) (2a-2)=0.?

又∵2^x+1≠0,∴2a-2=0,即a=1.?

由此可解得f ^-1 (x)=log₂.?

又∵2^x= ＞0,?

∴-1＜y＜1.因此y=f ^-1(x)的定义域为x∈(-1,1).?

（2）∵当x∈［，］时，f ^-1(x)≤g(x)恒成立，?

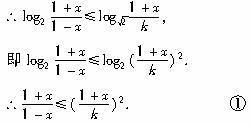
又由对数定义可知＞0,?

且由x∈［，］知1+x＞0,1-x＞0.故有k＞0.?

∴不等式①可化为k²≤1-x².?

令h(x)=1-x²,由二次函数的单调性可知h(x)在［，］上为单调减函数，

则有［h(x)］_min=h()=1-()²=.?

∴应有k²≤［h(x)］_min=.?

又∵k＞0,?

∴k的取值范围是0＜k≤.