题目内容
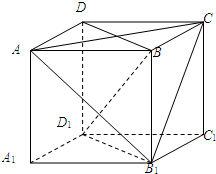 如图,棱长为1的正方体ABCD-A1B1C1D1中,
如图,棱长为1的正方体ABCD-A1B1C1D1中,(Ⅰ)求证:AC⊥平面BDD1B1;
(Ⅱ)求AB1与平面BDD1B1所成角的余弦值.
分析:(Ⅰ)由DD1⊥面AC,知DD1⊥AC,由DD1⊥BD,能够证明AC⊥平面BDD1B1.
(Ⅱ)利用AC⊥平面BDD1B1,可得∠AB1O为直线AB1与平面BDD1B1所成的角,通过解三角形可得结论;
(Ⅱ)利用AC⊥平面BDD1B1,可得∠AB1O为直线AB1与平面BDD1B1所成的角,通过解三角形可得结论;
解答: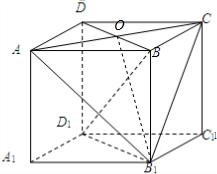 解:(Ⅰ)证明:∵DD1⊥面AC,AC?平面AC,∴DD1⊥AC,
解:(Ⅰ)证明:∵DD1⊥面AC,AC?平面AC,∴DD1⊥AC,
∵AC⊥BD,DD1∩BD=D,BD?平面BDD1B1,DD1?平面BDD1B1
∴AC⊥平面BDD1B1.
(Ⅱ)连结AC,BD交于O,
∵AO⊥平面BDD1B1,连结OB1,A在平面BDD1B1上的射影为为O,
∴∠AB1O为直线AB1与平面BDD1B1所成的角,
OB1=
=
=
,AB1=
在Rt△AB1O中,cos∠AB1O=
=
=
.
∴AB1与平面BDD1B1所成角的余弦值为
;
 解:(Ⅰ)证明:∵DD1⊥面AC,AC?平面AC,∴DD1⊥AC,
解:(Ⅰ)证明:∵DD1⊥面AC,AC?平面AC,∴DD1⊥AC,∵AC⊥BD,DD1∩BD=D,BD?平面BDD1B1,DD1?平面BDD1B1
∴AC⊥平面BDD1B1.
(Ⅱ)连结AC,BD交于O,
∵AO⊥平面BDD1B1,连结OB1,A在平面BDD1B1上的射影为为O,
∴∠AB1O为直线AB1与平面BDD1B1所成的角,
OB1=
| OB2+BB12 |
12+(
|
| ||
| 2 |
| 2 |
在Rt△AB1O中,cos∠AB1O=
| OB1 |
| AB1 |
| ||||
|
| ||
| 2 |
∴AB1与平面BDD1B1所成角的余弦值为
| ||
| 2 |
点评:本题考查直线与平面垂直的证明.解题时要认真审题,仔细解答,注意合理地进行等价转化,解题的关键是正确作出空间角

练习册系列答案
相关题目
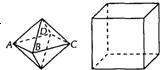


 两个相同的正四棱锥组成如图所示的几何体,可放入棱长为
两个相同的正四棱锥组成如图所示的几何体,可放入棱长为