题目内容
正项数列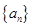 满足
满足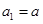 ,
,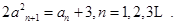
(1)若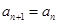 ,求
,求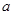 的值;
的值;
(2)当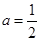 时,证明:
时,证明: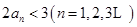 ;
;
(3)设数列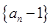 的前
的前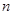 项之积为
项之积为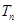 ,若对任意正整数
,若对任意正整数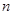 ,总有
,总有 成立,求
成立,求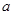 的取值范围
的取值范围
【答案】
(1)
(2) ;
;
(3)实数 的取值范围是
的取值范围是
【解析】(1)因为 所以
所以 ,解得
,解得 或
或 (舍去)
(舍去)
由 的任意性知,
的任意性知, ……………3分
……………3分
(2)反证法:假设 ……………4分
……………4分
即 ,则
,则 得
得
依此类推, 这与
这与 矛盾。
矛盾。
所以假设不成立,则 ……………7分
……………7分
(3)由题知,当 时,
时, ,
,
所以
同理有
将上述 个式子相乘,得
个式子相乘,得 ,
,
即 ……………11分
……………11分
当 时,
时, 也成立,
也成立,
所以 ……………12分
……………12分
从而要使 对任意的
对任意的 恒成立,
恒成立,
只要使 对任意的
对任意的 恒成立即可。
恒成立即可。
因为数列 单调递增,所以
单调递增,所以 ……………13分
……………13分
即
所以实数 的取值范围是
的取值范围是
又a>0,
所以实数 的取值范围是
的取值范围是 ………14分
………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足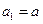 ,
,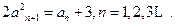
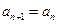 ,求
,求 的值;
的值;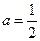 时,证明:
时,证明: ;
; 的前
的前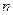 项之积为
项之积为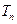 ,若对任意正整数
,若对任意正整数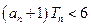 成立,求
成立,求 满足:
满足: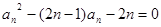 .
.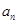 ;
;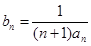 ,求数列
,求数列 项和
项和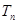 .
.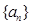 满足:
满足:
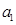 的范围,使得
的范围,使得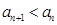 恒成立;
恒成立; ,证明
,证明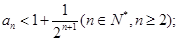
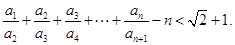
 满足:
满足:
 的范围,使得
的范围,使得 恒成立;
恒成立; ,证明
,证明
