题目内容
不等式 对
对 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( )
A. | B. | C.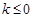 | D. |
C
解析试题分析:因为 对
对 恒成立,即
恒成立,即 对
对 恒成立,令
恒成立,令 ,只需
,只需 ,所以
,所以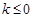 。
。
考点:指数函数的性质;一元二次不等式的解法;一元二次方程跟的分布。
点评:做此题的关键是把不等式 对
对 恒成立,转化为
恒成立,转化为 对
对 恒成立。一定要注意
恒成立。一定要注意 这个条件。
这个条件。

练习册系列答案
相关题目
已知 ,且
,且 为幂函数,则
为幂函数,则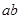 的最大值为
的最大值为
A. | B. | C. | D. |
若 ,则
,则 的解集为 ( )
的解集为 ( )
A. | B. | C. | D. |
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A. | B. | C. 和 和 | D. |
方程 的根所在的区间为 ( )
的根所在的区间为 ( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
已知定义在R上的奇函数 ,满足
,满足 ,且在区间[0,2]上是减函数,则( )
,且在区间[0,2]上是减函数,则( )
A. | B. |
C. | D. |
函数 在
在 上恒为正数,则实数
上恒为正数,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数 的图像与
的图像与 轴的交点个数为 ( )
轴的交点个数为 ( )
| A.一个 | B.至少一个 | C.至多两个 | D.至多一个 |
f(x)= ,则f{f[f(-3)]}等于
,则f{f[f(-3)]}等于
| A.0 | B.π | C.π2 | D.9 |