Question

【题目】已知数列为递增的等差数列，，，，其中．

（1）求数列的通项公式；

（2）设，求数列的前项和；

（3）设，求使不等式对一切均成立的最大实数．

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）利用函数解析式可得到，由等查查中项定义可构造方程求得，由数列单调性确定后可求得；由等差数列通项公式可求得结果；

（2）由（1）可得，采用错位相减法可求得结果；

（3）分离变量将问题变为恒成立；令不等式右侧为，通过可知单调递增，由此可知，进而得到结果.

（1）由题意得：，

，

为等差数列，，即，

解得：或，

当时，，，；当时，，，；

为递增数列，，公差，

；

（2）由（1）得：

…①

则…②

①②得：

，

；

（3）由题意得：对恒成立

由（1）知：，

记，

，

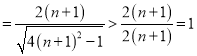，，即单调递增，

的最小值为，，即．