题目内容
设曲线y=(ax-1)ex在点A(x0,y1)处的切线为l1,曲线y=(1-x)e-x在点B(x0,y2)处的切线为l2.若存在x0∈[0,
],使得l1⊥l2,则实数a的取值范围为______.
| 3 |
| 2 |
函数y=(ax-1)ex的导数为y′=(ax+a-1)ex,
∴l1的斜率为k1=(ax0+a-1)ex0,
函数y=(1-x)e-x的导数为y′=(x-2)e-x
∴l2的斜率为k2=(x0-2)e-x0,
由题设有k1•k2=-1从而有(ax0+a-1)ex0•(x0-2)e-x0=-1
∴a(x02-x0-2)=x0-3
∵x0∈[0,
]得到x02-x0-2≠0,所以a=
,
又a′=
,另导数大于0得1<x0<5,
故
在(0,1)是减函数,在(1,
)上是增函数,
x0=0时取得最大值为
=
;
x0=1时取得最小值为1.
∴1≤a≤
故答案为:1≤a≤
∴l1的斜率为k1=(ax0+a-1)ex0,
函数y=(1-x)e-x的导数为y′=(x-2)e-x
∴l2的斜率为k2=(x0-2)e-x0,
由题设有k1•k2=-1从而有(ax0+a-1)ex0•(x0-2)e-x0=-1
∴a(x02-x0-2)=x0-3
∵x0∈[0,
| 3 |
| 2 |
| x0-3 | ||
|
又a′=
| -(x0-1)(x0-5) | ||
(
|
故
| x0-3 | ||
|
| 3 |
| 2 |
x0=0时取得最大值为
| 0-3 |
| 02-0-2 |
| 3 |
| 2 |
x0=1时取得最小值为1.
∴1≤a≤
| 3 |
| 2 |
故答案为:1≤a≤
| 3 |
| 2 |

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
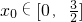 ,使得l1⊥l2,求实数a的取值范围.
,使得l1⊥l2,求实数a的取值范围. ,使得l1⊥l2,则实数a的取值范围为 .
,使得l1⊥l2,则实数a的取值范围为 .