题目内容
设曲线y=(ax-1)ex在点A(x0,y1)的切线为l1,曲线y=
在点B(x0,y2)的切线为l2,若存在x0∈[-
,
],使得l1⊥l2,则实数a的取值范围是
| 1-x |
| ex |
| 1 |
| 2 |
| 3 |
| 2 |
[1,
]
| 14 |
| 5 |
[1,
]
.| 14 |
| 5 |
分析:利用导数的几何意义可得kl1,kl2.存在x0∈[-
,
],使得l1⊥l2,可得(ax0+a-1)ex0•
=-1在x0∈[-
,
]有解.化为a=
,x0∈[-
,
].再利用导数研究其单调性即可.
| 1 |
| 2 |
| 3 |
| 2 |
| x0-2 |
| ex0 |
| 1 |
| 2 |
| 3 |
| 2 |
| x0-3 |
| (x0+1)(x0-2) |
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:对于曲线y=(ax-1)ex,y′=(ax+a-1)ex,∴kl1=(ax0+a-1)ex0.
对于曲线y=
,y′=
,∴kl2=
.
∵存在x0∈[-
,
],使得l1⊥l2,∴(ax0+a-1)ex0•
=-1在x0∈[-
,
]有解.
化为a=
,x0∈[-
,
].
a′=
,
当x0∈[-
,1)时,a′<0,函数a单调递减;当x0∈(1,
]时,a′>0,函数a单调递增.
因此函数a在x0=1时取得最小值,a(1)=1;
又a(-
)=
,a(
)=
,因此函数a的最大值为a(-
)=
.
∴实数a的取值范围是[1,
].
故答案为[1,
].
对于曲线y=
| 1-x |
| ex |
| x-2 |
| ex |
| x0-2 |
| ex0 |
∵存在x0∈[-
| 1 |
| 2 |
| 3 |
| 2 |
| x0-2 |
| ex0 |
| 1 |
| 2 |
| 3 |
| 2 |
化为a=
| x0-3 |
| (x0+1)(x0-2) |
| 1 |
| 2 |
| 3 |
| 2 |
a′=
| -(x0-1)(x0-5) |
| (x0+1)2(x0-2)2 |
当x0∈[-
| 1 |
| 2 |
| 3 |
| 2 |
因此函数a在x0=1时取得最小值,a(1)=1;
又a(-
| 1 |
| 2 |
| 14 |
| 5 |
| 3 |
| 2 |
| 6 |
| 5 |
| 1 |
| 2 |
| 14 |
| 5 |
∴实数a的取值范围是[1,
| 14 |
| 5 |
故答案为[1,
| 14 |
| 5 |
点评:本题考查了利用导数研究函数的单调性、几何意义、相互垂直的直线的斜率之间的关系,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
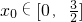 ,使得l1⊥l2,求实数a的取值范围.
,使得l1⊥l2,求实数a的取值范围. ,使得l1⊥l2,则实数a的取值范围为 .
,使得l1⊥l2,则实数a的取值范围为 .