题目内容
不等式组
|
①求a和M的值;
②在D中随机取一点P(x,y),求z≤
| M |
| 2 |
分析:①先根据a的不同取值画出可行域,再利用m=-4求出对应的a和M的值即可.(一定要分类讨论).
②由①的结论知分M的两种情况分别求出整个区域的面积和对应的点P所在区域的面积,再利用几何概型的计算公式求出z≤
的概率.
②由①的结论知分M的两种情况分别求出整个区域的面积和对应的点P所在区域的面积,再利用几何概型的计算公式求出z≤
| M |
| 2 |
解答: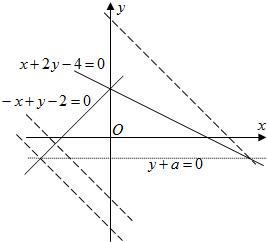 解:①如图,z=x+y的值就是平面上直线z=x+y在y轴上的截距,
解:①如图,z=x+y的值就是平面上直线z=x+y在y轴上的截距,
而且当P是直线y+a=0与直线-x+y-2=0的交点、直线y+a=0与直线x+2y-4=0的交点时,取得最大(小值).
解
得
,
解
得
z1=-2a-2,z2=a+4.
若z1>z2,即a<-2,则m=z2=-4,a=-8,M=z1=14;
若z1<z2,即a>-2,则m=z1=-4,a=1,M=z2=5.
所以,a=-8、M=14,或a=1、M=5.
②若a=-8、M=14,则z≤
即x+y≤7.直接计算知区域D的面积S=
×|[(2a+4)-(-a-2)]×(a+2)|=
(a+2)2=54,
区域D中x+y≤7部分的面积s=54-
=
,
所求概率p=
=
.
若a=1、M=5,则z≤
即x+y≤
.区域D的面积S=
,
区域D中x+y≤
部分的面积s=
-
=
,
所求概率p=
=
.
 解:①如图,z=x+y的值就是平面上直线z=x+y在y轴上的截距,
解:①如图,z=x+y的值就是平面上直线z=x+y在y轴上的截距,而且当P是直线y+a=0与直线-x+y-2=0的交点、直线y+a=0与直线x+2y-4=0的交点时,取得最大(小值).
解
|
|
解
|
|
z1=-2a-2,z2=a+4.
若z1>z2,即a<-2,则m=z2=-4,a=-8,M=z1=14;
若z1<z2,即a>-2,则m=z1=-4,a=1,M=z2=5.
所以,a=-8、M=14,或a=1、M=5.
②若a=-8、M=14,则z≤
| M |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
区域D中x+y≤7部分的面积s=54-
| 63 |
| 4 |
| 153 |
| 4 |
所求概率p=
| s |
| S |
| 17 |
| 24 |
若a=1、M=5,则z≤
| M |
| 2 |
| 5 |
| 2 |
| 27 |
| 2 |
区域D中x+y≤
| 5 |
| 2 |
| 27 |
| 2 |
| 15 |
| 8 |
| 93 |
| 8 |
所求概率p=
| s |
| S |
| 31 |
| 36 |
点评:这是含参数的、线性规划与几何概型的综合,解题关键是数形结合,能适时运用坐标的几何意义、点到直线距离或平行直线间的距离.

练习册系列答案
相关题目