题目内容
已知集合 ,
, .
.
(1)当 时,求
时,求 ;
;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)先计算出 , 当
, 当 时,再计算出
时,再计算出 ,进而求两个集合的公共部分即可求出
,进而求两个集合的公共部分即可求出 ;(2)法一:先将
;(2)法一:先将 变形为
变形为 ,然后针对两根
,然后针对两根 、
、 的大小分
的大小分 、
、 、
、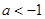 三类进行讨论,进而根据
三类进行讨论,进而根据 可求出
可求出 的取值范围;法二:根据
的取值范围;法二:根据 且
且 ,结合二次函数的图像与性质得到
,结合二次函数的图像与性质得到 ,从中求解即可得到
,从中求解即可得到 的取值范围.
的取值范围.
法一:(1) 2分
2分
当 时,
时, 4分
4分
∴ 6分
6分
(2) 7分
7分
①当 时,
时,
 不成立 9分
不成立 9分
②当 即
即 时,
时,
 ,
, ,解得
,解得 11分
11分
③当 即
即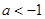 时,
时,
 解得
解得 13分
13分
综上,当 ,实数
,实数 的取值范围是
的取值范围是 14分(缺等号扣2分)
14分(缺等号扣2分)
法二:(1) 2分
2分
当 时,
时, 4分
4分
∴ 6分
6分
(2)记

 即
即 ,也就是
,也就是 10分
10分
解得 或
或
 实数
实数 的取值范围是
的取值范围是 14分 (缺等号扣2分).
14分 (缺等号扣2分).
考点:1.集合的运算;2.集合间的关系.

练习册系列答案
相关题目
 ,函数
,函数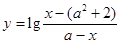 的定义域为集合B.
的定义域为集合B. 时,求集合
时,求集合 ;
; ,命题q:
,命题q:  ,若q是p的必要条件,求实数a的取值范围.
,若q是p的必要条件,求实数a的取值范围. ,B={x|m+1≤x≤2m-1}.
,B={x|m+1≤x≤2m-1}. ,
, .
. 时,求
时,求 和
和 ;
; ,求实数
,求实数 的取值范围.
的取值范围. B时,求a的取值范围.
B时,求a的取值范围. ,
, ,
, ,记
,记 ,
, ,并写出
,并写出 .
. ,集合
,集合 .
. ,
, ;
; ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围. ,
, ,则实数
,则实数 的取值范围是___________________.
的取值范围是___________________.