题目内容
∫-11(x3+x7cos4x)dx=________.
0
分析:被积函数x3+x7cos4x的原函数不好求,可根据函数x3+x7cos4x是奇函数,根据定积分的几何意义可得结论.
解答:因为函数x3+x7cos4x是奇函数,而积分上限和下限互为相反数
根据定积分的几何意义可知∫-11(x3+x7cos4x)dx表示函数x3+x7cos4x在x=-1,x=1与x轴围成图形的面积的代数和
∴∫-11(x3+x7cos4x)dx=0
故答案为:0
点评:本题主要考查了定积分,以及定积分的几何意义和奇函数的应用,属于基础题.
分析:被积函数x3+x7cos4x的原函数不好求,可根据函数x3+x7cos4x是奇函数,根据定积分的几何意义可得结论.
解答:因为函数x3+x7cos4x是奇函数,而积分上限和下限互为相反数
根据定积分的几何意义可知∫-11(x3+x7cos4x)dx表示函数x3+x7cos4x在x=-1,x=1与x轴围成图形的面积的代数和
∴∫-11(x3+x7cos4x)dx=0
故答案为:0
点评:本题主要考查了定积分,以及定积分的几何意义和奇函数的应用,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
某企业三月中旬生产A、B、C三种产品共3000件,根据分层抽样的结果,企业统计员制作了如下的统计表格:
| 产品类别 | A | B | C |
| 产品数量(件) | 1300 | ||
| 各层抽取件数 | 130 |
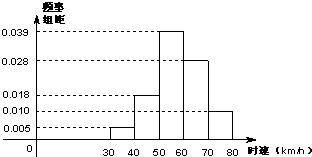 有100辆汽车在一个时段经过某一雷达测速区,这些汽车运行时速的频率分布直方图如图所示,则时速超过60km/h的汽车数量约为________辆.
有100辆汽车在一个时段经过某一雷达测速区,这些汽车运行时速的频率分布直方图如图所示,则时速超过60km/h的汽车数量约为________辆. 的定义域是集合A,函数g(x)=lg[x2-(2a+1)x+a2+a]的定义域是集合B.
的定义域是集合A,函数g(x)=lg[x2-(2a+1)x+a2+a]的定义域是集合B.

