题目内容
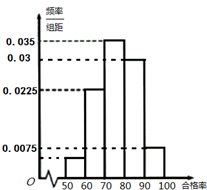
21、某工厂共有工人40人,在一次产品大检查中每人的产品合格率(百分比)绘制成频率分布直方图,如图所示.(Ⅰ)求合格率在[50,60)内的工人人数;
(Ⅱ)为了了解工人在本次大检查中产品不合格的情况,从合格率在[50,70)内的工人中随机选取3人的合格率进行分析,用X表示所选工人合格率在[60,70)内的人数,求X的分布列和数学期望.

【答案】分析:(Ⅰ)根据直方图,先求出产品合格率在[50,60)内的频率,进而可求产品合格率在[50,60)内的工人人数;
(Ⅱ)确定产品合格率在[50,70)内的工人人数为11人,X的可能取值是1,2,3,求出相应的概率,可得X的分布列和数学期望.
解答:解:(Ⅰ)产品合格率在[50,60)内的频率为1-(0.035+0.03+0.0225+0.0075)×10=0.05
∴产品合格率在[50,60)内的工人人数为40×0.05=2人;
(Ⅱ)同(Ⅰ)可得产品合格率在[60,70)内的工人人数为40×0.0225×10=9人,
∴产品合格率在[50,70)内的工人人数为11人
依题意,X的可能取值是1,2,3
P(X=1)=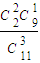 =
=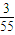 ;P(X=2)=
;P(X=2)=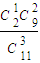 =
=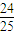 ;P(X=3)=
;P(X=3)=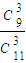 =
=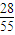
∴X的分布列为
∴EX=1×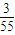 +2×
+2×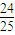 +3×
+3×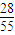 =
=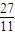 .
.
点评:本题考查频率直方图,考查离散型随机变量的分布列与期望,考查学生的计算能力,属于中档题.
(Ⅱ)确定产品合格率在[50,70)内的工人人数为11人,X的可能取值是1,2,3,求出相应的概率,可得X的分布列和数学期望.
解答:解:(Ⅰ)产品合格率在[50,60)内的频率为1-(0.035+0.03+0.0225+0.0075)×10=0.05
∴产品合格率在[50,60)内的工人人数为40×0.05=2人;
(Ⅱ)同(Ⅰ)可得产品合格率在[60,70)内的工人人数为40×0.0225×10=9人,
∴产品合格率在[50,70)内的工人人数为11人
依题意,X的可能取值是1,2,3
P(X=1)=
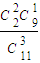 =
=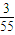 ;P(X=2)=
;P(X=2)=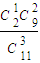 =
=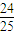 ;P(X=3)=
;P(X=3)=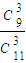 =
=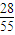
∴X的分布列为
| X | 1 | 2 | 3 |
| P | 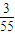 | 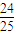 | 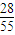 |
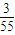 +2×
+2×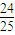 +3×
+3×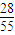 =
=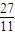 .
.点评:本题考查频率直方图,考查离散型随机变量的分布列与期望,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 (2012•福建模拟)21、某工厂共有工人40人,在一次产品大检查中每人的产品合格率(百分比)绘制成频率分布直方图,如图所示.
(2012•福建模拟)21、某工厂共有工人40人,在一次产品大检查中每人的产品合格率(百分比)绘制成频率分布直方图,如图所示. (2012•三明模拟)某工厂共有工人40人,在一次产品大检查中每人的产品合格率(百分比)绘制成频率分布直方图,如图所示.
(2012•三明模拟)某工厂共有工人40人,在一次产品大检查中每人的产品合格率(百分比)绘制成频率分布直方图,如图所示. 某工厂共有工人40人,在一次产品大检查中每人的产品合格率(百分比)绘制成频率分布直方图,如图所示.
某工厂共有工人40人,在一次产品大检查中每人的产品合格率(百分比)绘制成频率分布直方图,如图所示.