题目内容
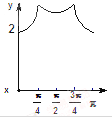
【题目】(2015·新课标I卷)函数f(x)=cos(![]() x+
x+![]() )的部分图像如图所示,则f(x)的单调递减区间为( )
)的部分图像如图所示,则f(x)的单调递减区间为( )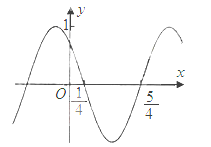
A.(k![]() -
-![]() ,k
,k![]() +
+![]() ), k
), k![]() Z
Z
B.(2k![]() -
-![]() ,2k
,2k![]() +
+![]() ),k
),k![]() Z
Z
C.(k-![]() ,k+
,k+![]() ), k
), k![]() Z
Z
D.(2k-![]() ,2k+
,2k+![]() ),k
),k![]() Z
Z
【答案】D
【解析】由五点作图知, 1 4 ω + φ = π 2 5 4 ω + φ = 3 π 2 ,解得 ω = π , φ = π 4 ,所以f(x)=cos( π x+ π 4 ),令2k π < π x+ π 4 ,k ∈ Z, 解得2k- 1 4 <x<2k+ 3 4 ,k ∈ Z ,故单调递减区间为(2k- 1 4 ,2k+ 3 4 ),k ∈ Z ,故选D。
本题考查函数y=Acos(ωx+φ)的图像与性质,先利用五点作图法列出关于 ω , φ 方程,求出 ω , φ 或利用利用图像先求出周期,用周期公式求出 ω ,利用特殊点求出 φ ,再利用复合函数单调性求其单调递减区间,是中档题,正确求 ω , φ 使解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目