题目内容
已知抛物线![]()
![]() 和直线
和直线![]() 没有公共点(其中
没有公共点(其中![]() 、
、![]() 为常数),动点
为常数),动点![]() 是直线
是直线![]() 上的任意一点,过
上的任意一点,过![]() 点引抛物线
点引抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 、
、![]() ,且直线
,且直线![]() 恒过点
恒过点![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知![]() 点为原点,连结
点为原点,连结![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点,证明:
两点,证明:![]() .
.
解:(1)如图,设![]() ,
,![]()
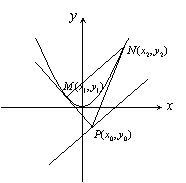 |
由![]() ,得
,得![]() ∴
∴![]() 的斜率为
的斜率为![]()
![]() 的方程为
的方程为![]() 同理得
同理得![]()
设![]() 代入上式得
代入上式得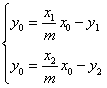 ,
,
即![]() ,
,![]() 满足方程
满足方程![]()
故![]() 的方程为
的方程为![]() ………………4分
………………4分
上式可化为![]() ,过交点
,过交点![]()
∵![]() 过交点
过交点![]() , ∴
, ∴![]() ,
,![]()
∴![]() 的方程为
的方程为![]() ………………6分
………………6分
(2)要证![]() ,即证
,即证![]()
设![]() ,
,![]()
则![]() ……(Ⅰ)
……(Ⅰ)
∵![]() ,
,![]()
∴![]() 直线方程为
直线方程为![]() ,
,
与![]() 联立化简
联立化简![]()
∴![]() ……①
……① ![]() ……② …………10分
……② …………10分
把①②代入(Ⅰ)式中,则分子
![]()
![]() …………(Ⅱ)
…………(Ⅱ)
又![]() 点在直线
点在直线![]() 上,∴
上,∴![]() 代入Ⅱ中得:
代入Ⅱ中得:
∴![]()
![]()
故得证 ………………14分

练习册系列答案
相关题目
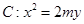
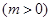 和直线
和直线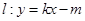 没有公共点(其中
没有公共点(其中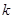 、
、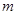 为常数),动点
为常数),动点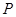 是直线
是直线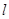 上的任意一点,过
上的任意一点,过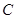 的两条切线,切点分别为
的两条切线,切点分别为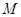 、
、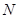 ,且直线
,且直线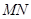 恒过点
恒过点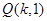 .
.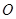 点为原点,连结
点为原点,连结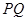 交抛物线
交抛物线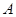 、
、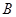 两点,证明:
两点,证明: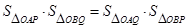 .
. 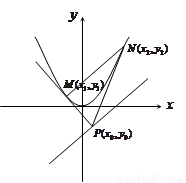
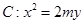
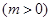 和直线
和直线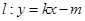 没有公共点(其中
没有公共点(其中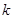 、
、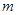 为常数),动点
为常数),动点 是直线
是直线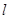 上的任意一点,过
上的任意一点,过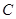 的两条切线,切点分别为
的两条切线,切点分别为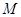 、
、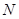 ,且直线
,且直线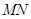 恒过点
恒过点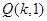 .
.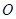 点为原点,连结
点为原点,连结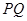 交抛物线
交抛物线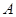 、
、 两点,
两点,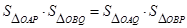

 和直线
和直线 没有公共点(其中
没有公共点(其中 、
、 为常数),动点
为常数),动点 是直线
是直线 上的任意一点,过
上的任意一点,过 的两条切线,切点分别为
的两条切线,切点分别为 、
、 ,且直线
,且直线 恒过点
恒过点 .
. 点为原点,连结
点为原点,连结 交抛物线
交抛物线 、
、 两点,
两点, .
.
 和直线
和直线 没有公共点(其中
没有公共点(其中 、
、 为常数),动点
为常数),动点 是直线
是直线 上的任意一点,过
上的任意一点,过 的两条切线,切点分别为
的两条切线,切点分别为 、
、 ,且直线
,且直线 恒过点
恒过点 .
. 点为原点,连结
点为原点,连结 交抛物线
交抛物线 、
、 两点,证明:
两点,证明: .
.
