题目内容
 直角梯形ABCD中,B,C为直角顶点,且AB<CD,动点P从点B(起点)出发,沿着拆线BCDA向点A(终点)运动.设点P运动的路程为x,△ABP的面积为f(x),若函数y=f(x)的图象如图所示,则△ABC的面积为( )
直角梯形ABCD中,B,C为直角顶点,且AB<CD,动点P从点B(起点)出发,沿着拆线BCDA向点A(终点)运动.设点P运动的路程为x,△ABP的面积为f(x),若函数y=f(x)的图象如图所示,则△ABC的面积为( )分析:首先根据图象可以得到BC=4,进而算出CD=5、AD=5.再作出梯形的高DE如图,△ADE中利用勾股定理算出AE=3,从而得到AB=8,最后用三角形面积公式可算出△ABC的面积.
解答:解:由图象知:当x=4和x=9时,△ABP的面积相等,
∴BC=4,BC+CD=9,解得CD=5,
又知AD=5,因此在直角梯形ABCD中AD=14-9=5,
如图,作DE⊥AB,
∵∠B=90°,
∴DE=BC=4,在Rt△AED中:AE=
=
=3,
因此,可得AB=AE+EB=3+5=8,
∴S△ABC=
AB•BC=
×8×4=16.
故选:D

∴BC=4,BC+CD=9,解得CD=5,
又知AD=5,因此在直角梯形ABCD中AD=14-9=5,
如图,作DE⊥AB,
∵∠B=90°,
∴DE=BC=4,在Rt△AED中:AE=
| AD2-DE2 |
| 25-16 |
因此,可得AB=AE+EB=3+5=8,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
故选:D
点评:本题给出关于梯形上动点,在已知动点路程与△ABP的面积的图象情况下,要我们求△ABC的面积.着重考查了勾股定理、面积公式的应用和函数图象的理解等知识,属于基础题.

练习册系列答案
相关题目
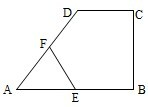 如图,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=
如图,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=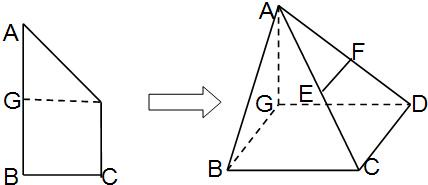
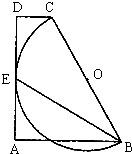 已知:如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,垂足为A,以腰BC为直径的半圆O切AD于点E,连接BE,若BC=6,∠EBC=30°,则梯形ABCD的面积为
已知:如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,垂足为A,以腰BC为直径的半圆O切AD于点E,连接BE,若BC=6,∠EBC=30°,则梯形ABCD的面积为 (2012•福建模拟)在直角梯形ABCD中,AD∥BC,BC=2AD=2AB=2
(2012•福建模拟)在直角梯形ABCD中,AD∥BC,BC=2AD=2AB=2