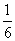题目内容
已知点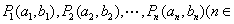
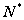
 在函数
在函数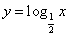 的图象上.
的图象上.
(1)若数列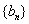 是等差数列,求证:数列
是等差数列,求证:数列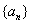 是等比数列;
是等比数列;
(2)若数列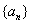 的前
的前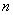 项和
项和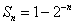 ,过点
,过点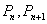 的直线与两坐标轴所围图形的面积为
的直线与两坐标轴所围图形的面积为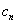 ,求最小的实数
,求最小的实数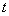 ,使得对任意的
,使得对任意的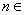
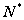 ,
,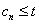 恒成立.
恒成立.
解:(1)设数列 的公比为
的公比为 ,则
,则 对
对 恒成立,依题意的
恒成立,依题意的 ,则
,则 ,所以
,所以 是非零常数,从而数列
是非零常数,从而数列 是等比数列.4分
是等比数列.4分
(2)当时 ,
, ,当
,当 时,
时, ,
, 也满足此式,
也满足此式,
所以数列 的通项公式是
的通项公式是 .…………6分
.…………6分
由 可得,
可得, .所以
.所以 .
.
从而过着两点的直线方程是 ,可得此直线与坐标轴的交点
,可得此直线与坐标轴的交点 .因此
.因此 ,…………10分
,…………10分
由于 ,所以数列
,所以数列 单调递减,即数列的
单调递减,即数列的 最大项为
最大项为 ,要使任意的
,要使任意的 ,
,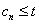 恒成立,只需
恒成立,只需 .所以实数
.所以实数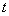 的最小值为
的最小值为 .……………………12分
.……………………12分

练习册系列答案
相关题目
 与双曲线
与双曲线 有相同的焦点
有相同的焦点 ,若
,若 是
是 的等比中项,
的等比中项, 是
是 与
与 的等差中项,则椭圆的离心率是
的等差中项,则椭圆的离心率是 B.
B. C.
C. D.
D.
 的最小值为
的最小值为 +2 B.
+2 B. 为平面,且m
为平面,且m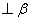 ,则“m//
,则“m//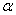 ”是“
”是“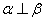 ”的充要条件;
”的充要条件;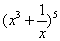 的展开式中含x3的项的系数为60;
的展开式中含x3的项的系数为60;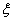 ~N(0,1),若P(
~N(0,1),若P(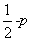 ;
;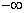 ,2);
,2);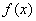 满足
满足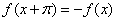 ,且0<x<
,且0<x<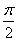 时
时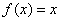 ,则函数
,则函数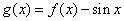 在[
在[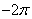 ,
,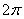 ]上有5个零点.
]上有5个零点. 中,
中, 为
为 上一点,且
上一点,且 ,
, 为
为 上一点,且
上一点,且 ,则
,则 取最小值时,向量
取最小值时,向量
 的模为 .
的模为 . ”的单调递增函数是( )
”的单调递增函数是( ) B.
B. C.
C. D.
D.
 是
是 上的增函数,
上的增函数, ,
, 是其图象上的两点,记不等式
是其图象上的两点,记不等式 <
< 的解集
的解集 ,则
,则

 B.
B. C.
C. D.
D.
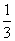 B.
B. 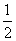 C.
C. 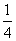 D.
D.