题目内容
13.函 数y=$\frac{{x}^{2}-x+n}{{x}^{2}+1}$(n∈N*,y≠1)的最大值为an,最小值为bn且cn=4(anbn-$\frac{1}{2}$)(1)求数列{cn}的通项公式;
(2)求f(n)=$\frac{{c}_{n}}{(n+36){c}_{n+1}}$(n∈N*)的最大值.
分析 (1)将函数化为关于x的方程,由方程有解的条件:判别式不小于0,结合y2-(n+1)y+n-$\frac{1}{4}$=0的两根为bn,an,运用韦达定理,即可得到所求通项公式;
(2)求得f(n),令4n-3=t(t≥1且t为正整数),可得n=$\frac{t+3}{4}$,化为t的关系式,再由基本不等式和对勾函数的性质,结合n为整数,即可得到所求最大值.
解答 解:(1)由已知,y=$\frac{{x}^{2}-x+n}{{x}^{2}+1}$(n∈N*,y≠1)的定义域为R,
则x2(y-1)+x+y-n=0方程有解,
即有△≥0即1-4(y-1)(y-n)≥0,
即y2-(n+1)y+n-$\frac{1}{4}$≤0的解集[bn,an],
即y2-(n+1)y+n-$\frac{1}{4}$=0的两根为bn,an,
可得anbn=n-$\frac{1}{4}$,
又因为cn=4(anbn-$\frac{1}{2}$),
则cn=4n-3,n∈N*;
(2)f(n)=$\frac{{c}_{n}}{(n+36){c}_{n+1}}$=$\frac{4n-3}{(n+36)(4n+1)}$
=$\frac{4n-3}{4{n}^{2}+145n+36}$,
令4n-3=t(t≥1且t为正整数),可得n=$\frac{t+3}{4}$,
则g(t)=$\frac{t}{\frac{(t+3)^{2}}{4}+\frac{145(t+3)}{4}+36}$
=$\frac{1}{t+\frac{588}{t}+151}$,
由t+$\frac{588}{t}$≥2$\sqrt{t•\frac{588}{t}}$=28$\sqrt{3}$,
当且仅当t=$\frac{588}{t}$,可得t=14$\sqrt{3}$,
当t=21时,n=6,t+$\frac{588}{t}$=49,
当t=22,23,24时,n不为整数;
当t=25时,n=7时,t+$\frac{588}{t}$=48+$\frac{13}{25}$;
则当n=7时,g(t)取得最大值,
即f(n)取得最大值$\frac{1}{48+\frac{13}{25}+151}$=$\frac{25}{4988}$.
点评 本题考查数列的通项公式的求法,注意运用函数方程的转化思想,考查数列的最大值的求法,注意运用基本不等式和对勾函数的性质,考查运算能力,属于中档题.

 小学课时特训系列答案
小学课时特训系列答案| A. | (0,2) | B. | (-2,3) | C. | (-2,0) | D. | (2,3) |
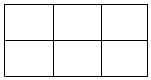 从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )
从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )| A. | 208 | B. | 204 | C. | 200 | D. | 196 |
| 教师 | 家长 | |
| 反对 | 40 | 20 |
| 支持 | 20 | 20 |
(2)把以上频率当概率,随机抽取3位教师,记其中反对学生带手机进校园的人数为X,求随机变量X的分布列和数学期望.
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
| A. | 若f(x)是奇函数,则f(f(x))也是奇函数 | |
| B. | 若f(x)是周期函数,则f(f(x))也是周期函数 | |
| C. | 若f(x)是单调递减函数,则f(f(x))也是单调递减函数 | |
| D. | 若方程f(x)=x有实根,则方程f(f(x))=x也有实根 |