题目内容
设数列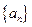 的前
的前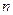 项和为
项和为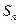 ,已知
,已知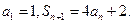
(1)设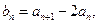 证明数列
证明数列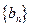 是等比数列;
是等比数列;
(2)求数列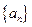 的通项公式;
的通项公式;
(3)求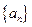 的前
的前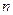 项和
项和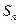 .
.
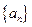 的前
的前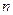 项和为
项和为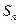 ,已知
,已知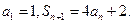
(1)设
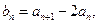 证明数列
证明数列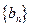 是等比数列;
是等比数列;(2)求数列
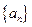 的通项公式;
的通项公式;(3)求
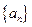 的前
的前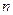 项和
项和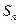 .
.(1)证明:由 ,及
,及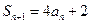 ,有
,有 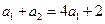 故
故 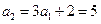
所以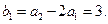
因为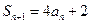 ①
①
故当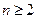 时,有
时,有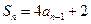 ②
②
①—②,得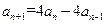
所以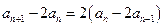
又因为 所以
所以 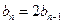
所以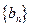 是首项为3,公比为2的等比数列. ………4分
是首项为3,公比为2的等比数列. ………4分
(2)解:由(1)可得: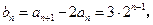
所以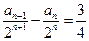
因此 数列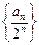 是首项为
是首项为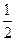 ,公差为
,公差为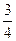 的等差数列.
的等差数列.
所以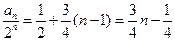
故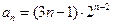 ………8分
………8分
(3)解:由 (1)知,当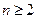 时,
时,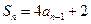
故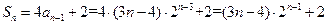 ,
,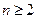
又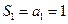
故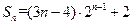 ,
,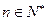 ………12分
………12分
 ,及
,及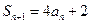 ,有
,有 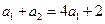 故
故 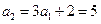
所以
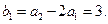
因为
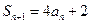 ①
① 故当
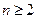 时,有
时,有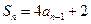 ②
②①—②,得
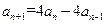
所以
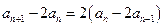
又因为
 所以
所以 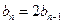
所以
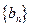 是首项为3,公比为2的等比数列. ………4分
是首项为3,公比为2的等比数列. ………4分(2)解:由(1)可得:
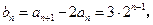
所以
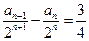
因此 数列
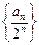 是首项为
是首项为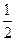 ,公差为
,公差为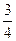 的等差数列.
的等差数列.所以
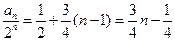
故
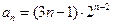 ………8分
………8分(3)解:由 (1)知,当
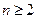 时,
时,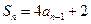
故
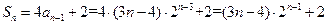 ,
,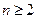
又
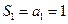
故
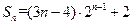 ,
,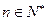 ………12分
………12分略

练习册系列答案
相关题目
 中,
中, ,则等差数列
,则等差数列 的前n项和为
的前n项和为 .已知
.已知
 求
求 和
和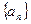 为等差数列,
为等差数列,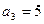 ,
,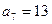 ,数列
,数列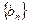 的前
的前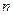 项和为
项和为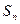 ,且有
,且有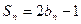
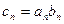 ,
,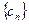 的前
的前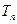 ,求
,求
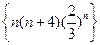 中的最大项是第
中的最大项是第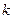 项,则
项,则 ).
).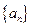 中,
中,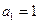 ,
,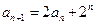 .
.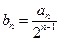 .证明:数列
.证明:数列 是等差数列;
是等差数列;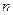 项和
项和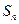 .
.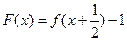 为R上的奇函数,
为R上的奇函数,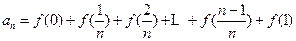
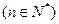 ,则数列
,则数列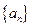 的通项公式为
的通项公式为


