题目内容
16.已知函数f(x)=2lnx+ax-$\frac{4f′(2)}{x}$(a∈R)在x=2处的切线经过点(-4,ln2)(1)讨论函数f(x)的单调性;
(2)若不等式$\frac{2xInx}{{1-{x^2}}}$>mx-1恒成立,求实数m的取值范围.
分析 (1)求出函数的导数,求出a的值,得到导函数的符号,求出函数的单调区间即可;
(2)问题转化为$\frac{1}{{1-{x^2}}}({2Inx+\frac{{1-{x^2}}}{x}})>m$,令$φ(x)=2Inx+\frac{{1-{x^2}}}{x}$$φ'(x)=\frac{2}{x}-\frac{1}{x^2}-1=-{({\frac{1}{x^2}-1})^2}≤0$,根据函数的单调性求出m的范围即可.
解答 解:(1)$f'(x)=\frac{2}{x}+a+\frac{4f'(2)}{x^2}$,令x=2,∴f'(2)=1+a+f'(2),
∴a=-1,设切点为(2,2ln2+2a-2f'(2)),
则y-(2ln2+2a-2f'(2))=f'(2)(x-2),
代入(-4,2ln2)得:2ln2-2ln2-2a+2f'(2)=-6f'(2),
∴$f'(2)=-\frac{1}{4}$,
∴$f'(x)=\frac{2}{x}-1-\frac{{-{{({x-1})}^2}}}{x^2}≤0$,
∴f(x)在(0,+∞)单调递减;
(2)$\frac{2xInx}{{1-{x^2}}}>mx-1$恒成立$\frac{1}{{1-{x^2}}}({2Inx+\frac{{1-{x^2}}}{x}})>m$,
令$φ(x)=2Inx+\frac{{1-{x^2}}}{x}$$φ'(x)=\frac{2}{x}-\frac{1}{x^2}-1=-{({\frac{1}{x^2}-1})^2}≤0$,
∴φ(x)在(0,+∞)单调递减,
∵φ(1)=0,
∴$\left\{\begin{array}{l}x∈({0,1}),φ(x)>0\\ x∈({1,+∞}),φ(x)<0\end{array}\right.$,
∴$\frac{1}{{1-{x^2}}}φ(x)$在(0,+∞)恒大于0,
∴m≤0.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.

| 班主任工作年限x(单位:年) | 4 | 6 | 8 | 10 | 12 |
| 被关注数量y(单位:百人) | 10 | 20 | 40 | 60 | 50 |
(2)若用$\frac{y_i}{x_i}$(i=1,2,3,4,5)表示统计数据时被关注数量的“即时均值”(四舍五入到整数),从“即时均值”中任选2组,求这2组数据之和小于8的概率.(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$).
| A. | 1026 | B. | 1025 | C. | 1024 | D. | 1023 |
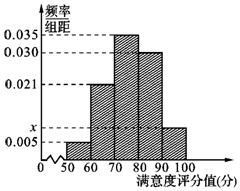 共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图.
共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图. 如图所示,在直角梯形ABEF中,将DCEF沿CD折起使∠FDA=60°,得到一个空间几何体.
如图所示,在直角梯形ABEF中,将DCEF沿CD折起使∠FDA=60°,得到一个空间几何体.