题目内容
(本小题满分13分)
已知⊙C经过点 、
、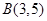 两点,且圆心C在直线
两点,且圆心C在直线 上.
上.
(1)求⊙C的方程;
(2)若直线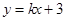 与⊙C总有公共点,求实数
与⊙C总有公共点,求实数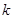 的取值范围.
的取值范围.
(1)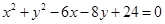 (2)
(2)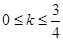
解析试题分析:(1)解法1:设圆的方程为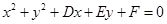 ,
,
则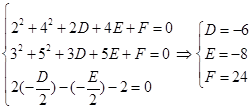 ,…………5分
,…………5分
所以⊙C方程为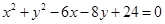 .………6分
.………6分
解法2:由于AB的中点为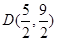 ,
, ,
,
则线段AB的垂直平分线方程为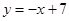
而圆心C必为直线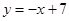 与直线
与直线 的交点,
的交点,
由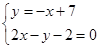 解得
解得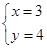 ,即圆心
,即圆心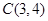 ,又半径为
,又半径为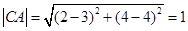 ,
,
故⊙C的方程为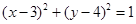 .
.
(2)解法1:因为直线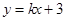 与⊙C总有公共点,
与⊙C总有公共点,
则圆心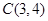 到直线
到直线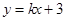 的距离不超过圆的半径,即
的距离不超过圆的半径,即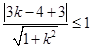 ,………11分
,………11分
将其变形得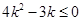 ,
,
解得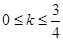 .………………13分
.………………13分
解法2:由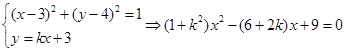 ,
,
因为直线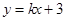 与⊙C总有公共点,则
与⊙C总有公共点,则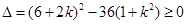 ,
,
解得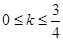 .
.
注:如有学生按这里提供的解法2答题,请酌情记分。
考点:本题考查了圆的方程及直线与圆的位置关系
点评:从直线和圆的位置关系的角度考查圆的方程是高考中常见的形式。研究直线和圆的位置关系的相关问题时通常采用“几何法”即抓住圆心到直线的的距离与半径的关系.

练习册系列答案
相关题目
 到定点
到定点 与到定点
与到定点 的距离之比为3.
的距离之比为3. ,若曲线C上恰有两个点到直线
,若曲线C上恰有两个点到直线 的距离为1,
的距离为1, 的取值范围。
的取值范围。 的距离等于
的距离等于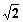 .
.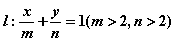 与圆C相切,求
与圆C相切,求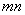 的最小值.
的最小值. 和点
和点 .
.
 向⊙
向⊙ 引切线
引切线 ,求直线
,求直线 截得的弦长为4的⊙
截得的弦长为4的⊙ 为(Ⅱ)中⊙
为(Ⅱ)中⊙ . 试探究:平面内是否存在一定点
. 试探究:平面内是否存在一定点 ,使得
,使得 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.  )(t∈R , t ≠ 0)为圆心的圆与
)(t∈R , t ≠ 0)为圆心的圆与 轴交于点O, A,
轴交于点O, A,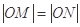 ,求圆C的方程.
,求圆C的方程. ,
, ).
).
 轴的正半轴建立平面直角坐标系,直线l的参数方程为
轴的正半轴建立平面直角坐标系,直线l的参数方程为 (t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
(t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
 .
.
 :
: 与圆
与圆 相交于
相交于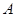 、
、 两点,求
两点,求 ;
; 、
、 是圆
是圆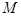 关于原点的对称点为
关于原点的对称点为 ,点
,点 轴的对称点为
轴的对称点为 ,如果直线
,如果直线 、
、 与
与 轴分别交于
轴分别交于 和
和 ,问
,问 是否为定值?若是求出该定值;若不是,请说明理由.
是否为定值?若是求出该定值;若不是,请说明理由. 个单位沿射线OM方向运动,设运动时间为t秒.问:当t为何值时直线PQ与圆C1相切?
个单位沿射线OM方向运动,设运动时间为t秒.问:当t为何值时直线PQ与圆C1相切?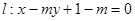
 ,圆
,圆 .
.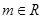 ,直线
,直线 与圆
与圆 恒有两个公共点.
恒有两个公共点.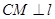 于点
于点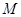 ,当
,当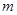 变化时,求点
变化时,求点 的方程.
的方程.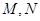 ,与圆
,与圆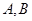 ,是否存在
,是否存在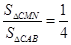 ?若存在,试求出
?若存在,试求出