题目内容
(本小题满分12分)
已知直线l:y=x,圆C1的圆心为(3,0),且经过(4,1)点.
(1)求圆C1的方程;
(2)若圆C2与圆C1关于直线l对称,点A、B分别为圆C1、C2上任意一点,求|AB|的最小值;
(3)已知直线l上一点M在第一象限,两质点P、Q同时从原点出发,点P以每秒1个单位的速度沿x轴正方向运动,点Q以每秒 个单位沿射线OM方向运动,设运动时间为t秒.问:当t为何值时直线PQ与圆C1相切?
个单位沿射线OM方向运动,设运动时间为t秒.问:当t为何值时直线PQ与圆C1相切?
(1)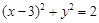 (2)
(2)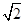 (3)
(3)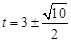
解析试题分析:(Ⅰ)依题意,设圆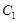 的方程为
的方程为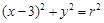 ………1分
………1分
∵ 圆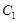 经过点
经过点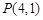
∴ 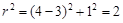 …………2分
…………2分
∴ 圆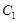 的方程为
的方程为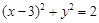 …………3分
…………3分
(Ⅱ)方法一:由(Ⅰ)可知,圆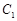 的圆心
的圆心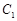 的坐标为
的坐标为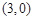 ,半径为
,半径为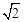
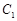 到直线
到直线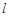 的距离
的距离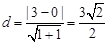 …………5分
…………5分
∴ 圆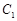 到直线的最短距离为
到直线的最短距离为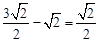 …………6分
…………6分
∵ 圆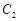 与圆
与圆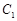 关于直线
关于直线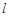 对称
对称
∴ 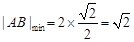 . …………7分
. …………7分
方法二:∵圆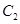 与圆
与圆 关于直线
关于直线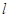 对称.
对称.
∴ 圆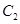 圆心为
圆心为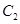 (0,3),半径为
(0,3),半径为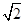 ……………5分
……………5分
∴ |
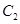 |=
|=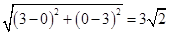
∴ 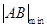 =
=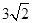 -2×
-2×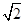 =
=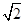 ………………7分
………………7分
(Ⅲ)当运动时间为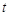 秒时,
秒时,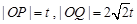 ,
,
则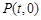 …………8分
…………8分
由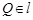 可设点
可设点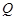 坐标为
坐标为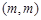 (
(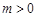 ),
),
则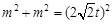
解得 ,即
,即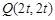
∴ 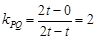
∴ 直线 方程为
方程为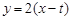 ,即
,即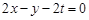 ……………10分
……………10分
若直线 与圆
与圆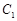 相切,则
相切,则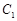 到直线
到直线 的距离
的距离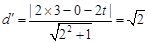 …………11分
…………11分
解得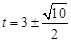
答:当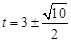 时,直线
时,直线 与圆
与圆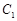 相切 …………12分
相切 …………12分
考点:利用点的对称求最值与圆的方程直线与圆的位置关系
点评:求与圆上的动点有关的距离最值问题通常先求出到圆心的距离

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 ,直线
,直线 过定点
过定点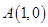 .
.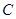 的坐标和圆的半径
的坐标和圆的半径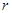 ;
; 面积的最大值,并求此时
面积的最大值,并求此时 、
、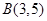 两点,且圆心C在直线
两点,且圆心C在直线 上.
上.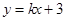 与⊙C总有公共点,求实数
与⊙C总有公共点,求实数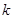 的取值范围.
的取值范围. |PD|.
|PD|.
 (极轴与x轴的非负半轴重合,且单位长度相同)。
(极轴与x轴的非负半轴重合,且单位长度相同)。 的距离; (2)若直线
的距离; (2)若直线 的值。
的值。 的圆形村落,
的圆形村落,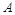 、
、 两人同时从村落中心出发。
两人同时从村落中心出发。 ,且后来
,且后来
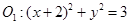 外切,与圆
外切,与圆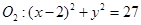 内切.
内切.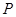 ,使直线
,使直线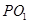 与
与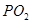 的斜率
的斜率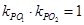 ?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标)
?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标)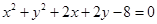 与圆C2:
与圆C2: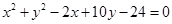 相交于A、B两点,
相交于A、B两点,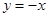 上,且经过A、B两点的圆的方程.
上,且经过A、B两点的圆的方程.  B = 90°,AC = 4,BC =
B = 90°,AC = 4,BC = 2,点P为线段CA(不包括端点)上的一个动点,以
2,点P为线段CA(不包括端点)上的一个动点,以 为圆心,1为半径作
为圆心,1为半径作 .
. ,若
,若 ,试判断
,试判断