题目内容
3.已知三棱锥A-BCD的所有顶点都在同一个球面上,△BCD是边长为2的正三角形,AC为球O的直径,若该三棱锥的体积为$\frac{{4\sqrt{2}}}{3}$,则该球O的表面积( )| A. | 64π | B. | 48π | C. | 32π | D. | 16π |
分析 根据题意作出图形,设球心为O,过BCD三点的小圆的圆心为O1,则OO1⊥平面BCD,延长CO1交球于点E,则AE⊥平面BCD,由该三棱锥的体积为$\frac{{4\sqrt{2}}}{3}$,求出AE=$\frac{4\sqrt{6}}{3}$,由AC为球O的直径,求出OO1=$\frac{1}{2}AE$=$\frac{2\sqrt{6}}{3}$,再求出CO1=$\frac{2\sqrt{3}}{3}$,从而求出球半径R=OC,进而能求出该球O的表面积.
解答 解:根据题意作出图形: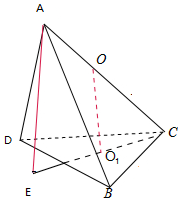 设球心为O,过BCD三点的小圆的圆心为O1,则OO1⊥平面BCD,
设球心为O,过BCD三点的小圆的圆心为O1,则OO1⊥平面BCD,
延长CO1交球于点E,则AE⊥平面BCD.
∵该三棱锥的体积为$\frac{{4\sqrt{2}}}{3}$,
∴$\frac{1}{3}×AE×{S}_{△BCD}$=$\frac{1}{3}×AE×\frac{1}{2}×2×2×sin60°$=$\frac{4\sqrt{2}}{3}$,
解得AE=$\frac{4\sqrt{6}}{3}$,
∵AC为球O的直径,∴OO1=$\frac{1}{2}AE$=$\frac{2\sqrt{6}}{3}$,
∵CO1=$\frac{2}{3}×\sqrt{4-1}$=$\frac{2\sqrt{3}}{3}$,∴球半径R=OC=$\sqrt{(\frac{2\sqrt{6}}{3})^{2}+(\frac{2\sqrt{3}}{3})^{2}}$=2.
∴该球O的表面积S=4πR2=16π.
故选:D.
点评 本题考查球的表面积的求法,考查三棱锥的外接球、球的表面积、三棱锥的体积等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.某冻品店为了解气温对其销售量的影响,随机记录了该店1月份中5天的日销售量y(单位:千克)与该地当日最低气温x(单位:℃)的数据作为样本,如表:
(1)利用最小二乘法求出y与x的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(2)设该地1月份的日最低气温X~N(μx,σx2),其中μx近似为样本平均数$\overline{x}$,σx2近似为样本方差Sx2,该地1月份的最高气温ξ与最低气温x的关系为ξ=2x+1且ξ~N(μξ,σξ2,)),其中μξ近似为最高气温的平均数,σξ2近似为最高气温的方差sξ2,求p(10.4≤ξ≤24.2).
附:①$\sqrt{130}$≈11.5,$\sqrt{3.2}$≈1.8,若X~N(μ,σ2),
则p(μ-σ≤ξ≤μ+σ)=0.6826,p(μ-2σ≤ξ≤μ+2σ)=0.9544
附:②回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$x.
| x | 3 | 6 | 9 | 8 | 9 |
| y | 12 | 10 | 8 | 8 | 7 |
(2)设该地1月份的日最低气温X~N(μx,σx2),其中μx近似为样本平均数$\overline{x}$,σx2近似为样本方差Sx2,该地1月份的最高气温ξ与最低气温x的关系为ξ=2x+1且ξ~N(μξ,σξ2,)),其中μξ近似为最高气温的平均数,σξ2近似为最高气温的方差sξ2,求p(10.4≤ξ≤24.2).
附:①$\sqrt{130}$≈11.5,$\sqrt{3.2}$≈1.8,若X~N(μ,σ2),
则p(μ-σ≤ξ≤μ+σ)=0.6826,p(μ-2σ≤ξ≤μ+2σ)=0.9544
附:②回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$x.
11.在△ABC中,A=$\frac{π}{6}$,AB=2,AC=3,点M在BC上且满足$\overrightarrow{CM}$=2$\overrightarrow{MB}$,则$\overrightarrow{AM}$$•\overrightarrow{BC}$=( )
| A. | $\frac{1}{3}$+$\sqrt{3}$ | B. | $\frac{1}{3}$-$\sqrt{3}$ | C. | $\frac{11}{3}$+$\sqrt{3}$ | D. | $\frac{11}{3}$-$\sqrt{3}$ |
13.如果P,P2,…Pn是抛物线C=y2=8x上的点,它们的横坐标依次为:x1,x2,…,xn,F是抛物线C的焦点,若x1+x2+…+xn=2017,|P1F|+|P2F|+…+|PnF|=( )
| A. | n+2017 | B. | n+4034 | C. | 2n+2017 | D. | 2n+4034 |