题目内容
已知正项数列{an}的前n项和为Sn,且an和Sn满足:4Sn=(an+1)2(n=1,2,3……),
(1)求{an}的通项公式;
(2)设bn= ,求{bn}的前n项和Tn;
,求{bn}的前n项和Tn;
(3)在(2)的条件下,对任意n∈N*,Tn> 都成立,求整数m的最大值.
都成立,求整数m的最大值.
∵4Sn=(an+1)2, ①
∴4Sn-1=(an-1+1)2(n≥2), ②
①-②得
4(Sn-Sn-1)=(an+1)2-(an-1+1)2.
∴4an=(an+1)2-(an-1+1)2.
化简得(an+an-1)·(an-an-1-2)=0.
∵an>0,∴an-an-1=2(n≥2).
∴{an}是以1为首项,2为公差的等差数列.
∴an=1+(n-1)·2=2n-1.
(2)bn= =
=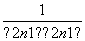 =
=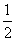 (
(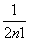 -
-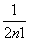 ).
).
∴Tn=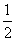
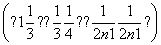
=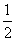 (1-
(1-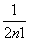 )=
)=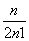
(3)由(2)知Tn=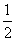 (1-
(1-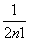 ),
),
Tn+1-Tn=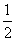 (1-
(1-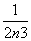 )-
)-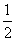 (1-
(1-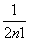 )
)
=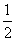 (
(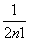 -
-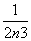 )>0.
)>0.
∴数列{Tn}是递增数列.
∴[Tn]min=T1=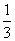 .
.
∴ <
<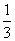 ,∴m<
,∴m<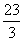 .
.
∴整数m的最大值是7.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 }满足
}满足  ,
, ,
, , ...,
, ...,  ,...,是首项为1,公比为2的等比数列,那么
,...,是首项为1,公比为2的等比数列,那么 中,
中, ,则
,则 的最大值为 .
的最大值为 .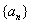 为等差数列,且
为等差数列,且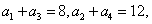
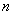 项和为
项和为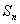 ,若
,若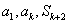 成等比数列,求正整数
成等比数列,求正整数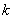 的值
的值 的值的一个程序框图,其中判断框内应填入的条件是( )
的值的一个程序框图,其中判断框内应填入的条件是( )  =50
=50
 程序框图如下:
程序框图如下: 的解集为____________.
的解集为____________. ,且
,且 则
则 = .
= .