题目内容
在极坐标系中，过点P(4，-
)与极轴所在直线垂直的直线方程是（ ）
| 2π |
| 3 |
分析：先将P化为直角坐标，再求出直线方程的直角坐标形式，最后化成极坐标形式．
解答：解：P(4，-
)的直角坐标为P(4cos(-
)，4sin(-
))，即P（-2，-2
）
过P与极轴所在直线垂直的直线方程为x=-2，
极坐标方程为ρcosθ=-2．
故选A．
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 3 |
过P与极轴所在直线垂直的直线方程为x=-2，
极坐标方程为ρcosθ=-2．
故选A．
点评：本题考查极坐标与直角坐标的转化，直角坐标与极坐标间的关系为：ρcosθ=x，ρsinθ=y，ρ2=x2+y2．
练习册系列答案
快捷英语周周练系列答案
相关题目
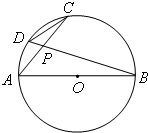（2007•深圳一模）请从下面两题中选做一题，如果两题都做，以第一题的得分为最后得分．